早教吧作业答案频道 -->数学-->
如图,四边形ABCD内接于O,对角线AC为O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求∠CDE的度数;(2)求证:DF是O的切线;(3)若AC=25DE,求tan∠ABD
题目详情
如图,四边形ABCD内接于 O,对角线AC为 O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
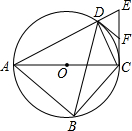
(1)求∠CDE的度数;
(2)求证:DF是 O的切线;
(3)若AC=2
DE,求tan∠ABD的值.

(1)求∠CDE的度数;
(2)求证:DF是 O的切线;
(3)若AC=2
| 5 |
▼优质解答
答案和解析
(1) ∵对角线AC为 O的直径,
∴∠ADC=90°,
∴∠EDC=90°;
(2)证明:连接DO,
∵∠EDC=90°,F是EC的中点,
∴DF=FC,
∴∠FDC=∠FCD,
∵OD=OC,
∴∠OCD=∠ODC,
∵∠OCF=90°,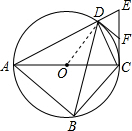
∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,
∴DF是 O的切线;
(3) 如图所示:可得∠ABD=∠ACD,
∵∠E+∠DCE=90°,∠DCA+∠DCE=90°,
∴∠DCA=∠E,
又∵∠ADC=∠CDE=90°,
∴△CDE∽△ADC,
∴
=
,
∴DC2=AD•DE
∵AC=2
DE,
∴设DE=x,则AC=2
x,
则AC2-AD2=AD•DE,
期(2
x)2-AD2=AD•x,
整理得:AD2+AD•x-20x2=0,
解得:AD=4x或-5x(负数舍去),
则DC=
=2x,
故tan∠ABD=tan∠ACD=
=
=2.
∴∠ADC=90°,
∴∠EDC=90°;
(2)证明:连接DO,
∵∠EDC=90°,F是EC的中点,
∴DF=FC,
∴∠FDC=∠FCD,
∵OD=OC,
∴∠OCD=∠ODC,
∵∠OCF=90°,

∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,
∴DF是 O的切线;
(3) 如图所示:可得∠ABD=∠ACD,
∵∠E+∠DCE=90°,∠DCA+∠DCE=90°,
∴∠DCA=∠E,
又∵∠ADC=∠CDE=90°,
∴△CDE∽△ADC,
∴
| DC |
| AD |
| DE |
| DC |
∴DC2=AD•DE
∵AC=2
| 5 |
∴设DE=x,则AC=2
| 5 |
则AC2-AD2=AD•DE,
期(2
| 5 |
整理得:AD2+AD•x-20x2=0,
解得:AD=4x或-5x(负数舍去),
则DC=
(2
|
故tan∠ABD=tan∠ACD=
| AD |
| DC |
| 4x |
| 2x |
看了如图,四边形ABCD内接于O,...的网友还看了以下:
f(x)=∫(0,2x)f(t/2)dt+ln2,显然f(0)=ln2两边求导f'(x)=f(2x/ 2020-03-31 …
这5道题用波兰式表达(1)A*(B-C)+T/(D+E)-F/(S*H)(2)A/(B*C(E+F 2020-07-08 …
针对程序段:IF(A||B||C)THENW=W/X,对于(A,B,C)的取值,(57)测试用例能 2020-07-10 …
变限积分[a,b]上的积分∫[f(x+h)-f(x)]dx令x+h=t,那原式=∫[a+h,b+h 2020-07-11 …
∫(0→-x)f(t)dt=∫(0→x)f(-t)d(-t)为什么? 2020-07-16 …
求助微积分强人帮忙解这个二阶方程f"(t)=a1=(π〖d/2〗^2P(t)-k[x+f(t)]- 2020-07-31 …
已知函数f(x)的定义域为D,若存在非零常数t,使得对于任意x∈M(M⊆D),有x+t∈D,且f( 2020-08-01 …
(2012•湛江一模)已知函数f(x)的图象在[a,b]上连续不断曲线,定义:f1(x)=min{f 2020-11-12 …
(2014•临沂三模)设函数f(x)的定义域为D,若存在非零实数t使得对于任意x∈M(M⊆D),有x 2020-11-13 …
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于点O、A,直线x= 2020-12-23 …