早教吧作业答案频道 -->数学-->
在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.(1)如图1,直接写出∠ABD和∠CFE的度数;(2)图1中:AE和CF有什么
题目详情
在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
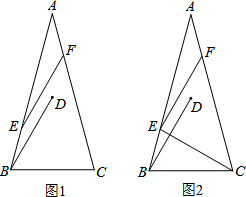
(1)如图1,直接写出∠ABD和∠CFE的度数;
(2)图1中:AE和CF有什么数量关系?请说明理由;
(3)如图2,连接CE,判断△CEF的形状并加说明理由.

(1)如图1,直接写出∠ABD和∠CFE的度数;
(2)图1中:AE和CF有什么数量关系?请说明理由;
(3)如图2,连接CE,判断△CEF的形状并加说明理由.
▼优质解答
答案和解析
(1)∵线段BC逆时针旋转旋转60°得到BD,
∴∠CBD=60°,
∵AB=AC,∠A=30°,
∴∠ABC=
=75°,
∴∠ABD=∠ABC-∠DBC=75°-60°=15°,
∵BD平移得到EF,
∴EF∥BD,
∴∠AEF=∠ABD=15°,
∵∠A=30°,
∴∠CFE=∠A+∠AEF=30°+15°=45°;
(2)AE=CF.
理由:如图1,连结CD、DF,
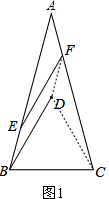
∵线段BC绕点B逆时针旋转60°得到线段BD,
∴BD=BC,∠CBD=60°,
∴△BCD是等边三角形,
∴CD=BD,
∵线段BD平移到EF,
∴EF∥BD,EF=BD,
∴四边形BDFE是平行四边形,EF=CD,
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
∴∠ABD=∠ABC-∠CBD=15°=∠ACD,
∴∠DFE=∠ABD=15°,∠AEF=∠ABD=15°,
∴∠AEF=∠ACD=15°,
∵∠CFE=∠A+∠AEF=30°+15°=45°,
∴∠CFD=∠CFE-∠DFE=45°-15°=30°,
∴∠A=∠CFD=30°,
在△AEF和△FCD中
∴△AEF≌△FCD(AAS),
∴ΑE=CF;
(3)△CEF是等腰直角三角,
理由如下:
如图2,过点E作EG⊥CF于G,
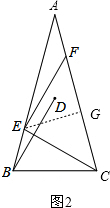
∵∠CFE=45°,
∴∠FEG=45°,
∴EG=FG,
∵∠A=30°,∠AGE=90°,
∴EG=
AE,
∵ΑE=CF,
∴EG=
CF,
∴FG=
CF,
∴G为CF的中点,
∴EG为CF的垂直平分线,
∴EF=EC,
∴∠CEF=2∠FEG=90°,
∴△CEF是等腰直角三角形.
(1)∵线段BC逆时针旋转旋转60°得到BD,
∴∠CBD=60°,
∵AB=AC,∠A=30°,
∴∠ABC=
| 180°-30° |
| 2 |
∴∠ABD=∠ABC-∠DBC=75°-60°=15°,
∵BD平移得到EF,
∴EF∥BD,
∴∠AEF=∠ABD=15°,
∵∠A=30°,
∴∠CFE=∠A+∠AEF=30°+15°=45°;
(2)AE=CF.
理由:如图1,连结CD、DF,

∵线段BC绕点B逆时针旋转60°得到线段BD,
∴BD=BC,∠CBD=60°,
∴△BCD是等边三角形,
∴CD=BD,
∵线段BD平移到EF,
∴EF∥BD,EF=BD,
∴四边形BDFE是平行四边形,EF=CD,
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
∴∠ABD=∠ABC-∠CBD=15°=∠ACD,
∴∠DFE=∠ABD=15°,∠AEF=∠ABD=15°,
∴∠AEF=∠ACD=15°,
∵∠CFE=∠A+∠AEF=30°+15°=45°,
∴∠CFD=∠CFE-∠DFE=45°-15°=30°,
∴∠A=∠CFD=30°,
在△AEF和△FCD中
|
∴△AEF≌△FCD(AAS),
∴ΑE=CF;
(3)△CEF是等腰直角三角,
理由如下:
如图2,过点E作EG⊥CF于G,

∵∠CFE=45°,
∴∠FEG=45°,
∴EG=FG,
∵∠A=30°,∠AGE=90°,
∴EG=
| 1 |
| 2 |
∵ΑE=CF,
∴EG=
| 1 |
| 2 |
∴FG=
| 1 |
| 2 |
∴G为CF的中点,
∴EG为CF的垂直平分线,
∴EF=EC,
∴∠CEF=2∠FEG=90°,
∴△CEF是等腰直角三角形.
看了在△ABC中,AB=AC,∠A...的网友还看了以下:
矩形ABCD的顶点A与坐标原点重合,AB,CD分别在x轴.y轴的正半轴上,点B的坐标为(1,0)点 2020-05-20 …
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=kx(k≠0)的图象相交于A、B两点,与 2020-06-14 …
用竖式计算小数乘法,应让各数的()对齐.A.首位B.末位C.小数点D.数位对齐 2020-06-27 …
用竖式计算小数乘法,应让各数的()对齐.A.首位B.末位C.小数点D.数位对齐 2020-06-27 …
已知某二次函数的图象与x轴分别相交于点A(-3,0)和点B(1,0),与y轴相交于C(0,-3m) 2020-07-25 …
如图在平面直角坐标系xoy中点AB的坐标分别为(-1,0)(4,0)点D在y轴上AD平行于BC点E 2020-07-30 …
已知f'(x)在点x=0处连续,且lim(x→0)[f'(x)/ln(1+x)]=-1,则A.f( 2020-07-31 …
一日内最低、最高气温出现的时间是:[]A.12点和0点B.13点和1点C.午后2点和0点D.14点和 2020-12-01 …
一日内最低、最高气温出现的时间约为()A、12点和0点B、13点和1点C、午后2点和0点D、日出前后 2020-12-01 …
1已知A(-1,m)与B(2,m+3√3)是反比例函数Y=K/X(K≠0)图像上的两个点(1)求K的 2020-12-08 …