早教吧作业答案频道 -->数学-->
已知在△ABC中,AB=AC=8,BC=4,点P是边AC上的一个动点,∠APD=∠ABC,AD∥BC,连接DC.(1)如图1,如果DC∥AB,求AP的长;(2)如图2,如果直线DC与边BA的延长线交于点E,设AP=x,AE=y,求y关于x的
题目详情
已知在△ABC中,AB=AC=8,BC=4,点P是边AC上的一个动点,∠APD=∠ABC,AD∥BC,连接DC.
(1)如图1,如果DC∥AB,求AP的长;
(2)如图2,如果直线DC与边BA的延长线交于点E,设AP=x,AE=y,求y关于x的函数解析式,并写出它的定义域;
(3)如图3,如果直线DC与边BA的反向延长线交于点F,连接BP,当△CPD与△CBF相似时,试判断线段BP与线段CF的数量关系,并说明你的理由.
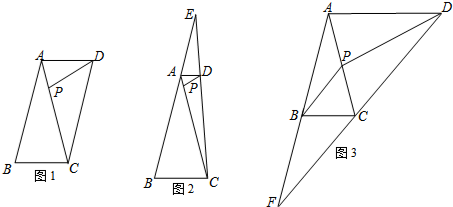
(1)如图1,如果DC∥AB,求AP的长;
(2)如图2,如果直线DC与边BA的延长线交于点E,设AP=x,AE=y,求y关于x的函数解析式,并写出它的定义域;
(3)如图3,如果直线DC与边BA的反向延长线交于点F,连接BP,当△CPD与△CBF相似时,试判断线段BP与线段CF的数量关系,并说明你的理由.

▼优质解答
答案和解析
(1)∵AD∥BC,
∴∠DAP=∠ACB,
∵∠APD=∠ABC,
∴△DPA∽△ABC,
∴
=
,
∵四边形ABCD是平行四边形,
∴AD=BC=4,
∵AB=AC=8,
∴
=
,
∴AP=2;
(2)由(1)得,
=
,
∴AD=2AP,
∵AD∥BC,
∴
=
,
∵AP=x,AE=y,
∴AD=2x,EB=y+8,
∴
=
,
∴y=
,它的定义域是0<x<2;
(3)BP=
CF;
∵∠APD=∠ABC,
∴∠DPC=∠FBC,
∵∠PCD>∠F,又△CPD与△CBF相似,
∴∠PCD=∠BCF,
∴△CPD∽△CBF,
∴
=
,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠APD=∠ABC,∠DAP=∠ACB,
∴∠DAP=∠APD,
∴AD=PD,
设AP=x,BF=y,则AD=PD=2x,AF=y+8,
∴
=
①,
∵AD∥BC,
∴
=
,
∴
=
②,
由①②得:x=4,y=8,
∴AP=PC=4,AB=BF=8,
∴BP是△ACF的中位线,
∴BP=
CF.
∴∠DAP=∠ACB,
∵∠APD=∠ABC,
∴△DPA∽△ABC,
∴
| AP |
| BC |
| AD |
| AC |
∵四边形ABCD是平行四边形,
∴AD=BC=4,
∵AB=AC=8,
∴
| AP |
| 4 |
| 4 |
| 8 |
∴AP=2;
(2)由(1)得,
| AP |
| BC |
| AD |
| AC |
∴AD=2AP,
∵AD∥BC,
∴
| AD |
| BC |
| AE |
| ED |
∵AP=x,AE=y,
∴AD=2x,EB=y+8,
∴
| 2x |
| 4 |
| y |
| y+8 |
∴y=
| 8x |
| 2-x |
(3)BP=
| 1 |
| 2 |
∵∠APD=∠ABC,
∴∠DPC=∠FBC,
∵∠PCD>∠F,又△CPD与△CBF相似,
∴∠PCD=∠BCF,
∴△CPD∽△CBF,
∴
| PD |
| BF |
| CP |
| BC |
∵AB=AC,
∴∠ABC=∠ACB,
∵∠APD=∠ABC,∠DAP=∠ACB,
∴∠DAP=∠APD,
∴AD=PD,
设AP=x,BF=y,则AD=PD=2x,AF=y+8,
∴
| 2x |
| y |
| 8-x |
| 4 |
∵AD∥BC,
∴
| BC |
| AD |
| BF |
| AF |
∴
| 4 |
| 2x |
| y |
| y+8 |
由①②得:x=4,y=8,
∴AP=PC=4,AB=BF=8,
∴BP是△ACF的中位线,
∴BP=
| 1 |
| 2 |
看了已知在△ABC中,AB=AC=...的网友还看了以下:
设事件AB满足P(A)=1/2,P(B)=1/3且P(A/B)+P(非A/非B)=1,则P(A+B 2020-04-06 …
为什么P(非A非B)=P[非(A+B)]为什么P(A)=P(AB)+P(A非B) 2020-04-26 …
P(A)=3/4,P(B)=5/6的条件下求P(A∩B)P(A)=3/4,P(B)=5/6的条件下 2020-05-19 …
事件A、B相互独立,已知P(A)=p,P(B)=q,求P(A∪非B),P(非A∪非B).最好明了清 2020-06-12 …
设A,B为任意两个事件且A⊂B,P(B)>0,则下列选项必然成立的是()A.P(A)<P(A|B) 2020-06-18 …
设A,B是两事件,已知P(A)=0.3,P(B)=0.6,试在下列两种情形下:(1)事件A,B互不 2020-06-22 …
P(A)=0.2,P(B)=0.45,P(AB)=0.15,求P(非A|非B),P(非A|B) 2020-07-19 …
请教三角形的几个己和恒等式的证明设I,O分别是三角形ABC的内心与外心,p为半周长,a、b、c为边 2020-08-03 …
设P是一个数集,且至少含有三个数,若对任意a,b∈P(a≠b)都有a+b,a-b、ab、ab∈P(除 2020-11-20 …
概率论与数理统计:设A包含于B,P(A)=0.2,P(B)=0.3求:(1)P(A并B)(2)P(A 2020-12-02 …