早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为.
题目详情
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为___.
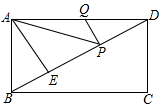

▼优质解答
答案和解析
设BE=x,则DE=3x,
∵四边形ABCD为矩形,且AE⊥BD,
∴△ABE∽△DAE,
∴AE2=BE•DE,即AE2=3x2,
∴AE=
x,
在Rt△ADE中,由勾股定理可得AD2=AE2+DE2,即62=(
x)2+(3x)2,解得x=
,
∴AE=3,DE=3
,
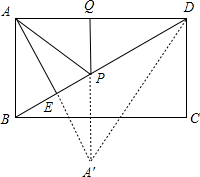
如图,设A点关于BD的对称点为A′,连接A′D,PA′,
则A′A=2AE=6=AD,AD=A′D=6,
∴△AA′D是等边三角形,
∵PA=PA′,
∴当A′、P、Q三点在一条线上时,A′P+PQ最小,
又垂线段最短可知当PQ⊥AD时,A′P+PQ最小,
∴AP+PQ=A′P+PQ=A′Q=DE=3
.
故答案是:3
.

设BE=x,则DE=3x,
∵四边形ABCD为矩形,且AE⊥BD,
∴△ABE∽△DAE,
∴AE2=BE•DE,即AE2=3x2,
∴AE=
| 3 |
在Rt△ADE中,由勾股定理可得AD2=AE2+DE2,即62=(
| 3 |
| 3 |
∴AE=3,DE=3
| 3 |
如图,设A点关于BD的对称点为A′,连接A′D,PA′,
则A′A=2AE=6=AD,AD=A′D=6,
∴△AA′D是等边三角形,
∵PA=PA′,
∴当A′、P、Q三点在一条线上时,A′P+PQ最小,
又垂线段最短可知当PQ⊥AD时,A′P+PQ最小,
∴AP+PQ=A′P+PQ=A′Q=DE=3
| 3 |
故答案是:3
| 3 |
看了如图,在矩形ABCD中,AD=...的网友还看了以下:
如图在三角形ABC中,D是BC上一点,E是AC上一点,且满足AD=AB,角ADE=角C1,如图在三 2020-05-15 …
如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.(1)请指出图中所有的相似三角形.如图 2020-05-16 …
关于数学试卷的难题在△ABC中,∠A=∠B=∠C,AB=6,AD⊥BC,垂足为D,则BD的长为 2020-06-27 …
已知锐角三角形ABC内接于O,AD⊥BC.垂足为D.(1)如图1,若AB=BC,BD=DC,求∠B 2020-07-19 …
在三角形ABC中,AB=AC,过A作AD⊥BC,垂足为D,E是AD上任意一点,过点E作EM⊥AB, 2020-07-22 …
如图在三角形abc中ab等于ac,AD垂直BC,垂足为D,三角形ABC的周长是36CM如图在三角形 2020-07-30 …
线段题分类讨论点C,D在直线AB上,线段AC,CB,AD,DB的长度满足AC:CB=5:4,AD: 2020-08-01 …
在三角形ABC中,角B=22.5度,AB的垂直平分线交AB于点Q,交BC于点P,PE垂直AC,垂足 2020-08-03 …
如图BC是○O的直径点A在○O上AD⊥BC垂足为D弧AE=弧ABBE分别交ADAC于点FG判断△AB 2020-11-03 …
已知,如图,在三角形abc中,角bac等于90度,ad垂直bc,垂足为d,e是ac中点,ed的延长已 2020-11-27 …