早教吧作业答案频道 -->数学-->
如图1,在Rt△ACB中,∠BAC=90°,AB=AC,分别过B、C两点作过点A的直线l的垂线,垂足为D、E;(1)如图1,当D、E两点在直线BC的同侧时,①猜想,BD、CE、DE三条线段有怎样的数量关系?并说明
题目详情
如图1,在Rt△ACB中,∠BAC=90°,AB=AC,分别过B、C两点作过点A的直线l的垂线,垂足为D、E;
(1)如图1,当D、E两点在直线BC的同侧时,①猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.②若线段BD=a,CE=b.请你求出△ABC的面积(用含a,b的代数式表示);
(2)如图2,当D、E两点在直线BC的两侧时,BD、CE、DE三条线段的数量关系为___;
(3)如图3,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?(直接写出结果即可)
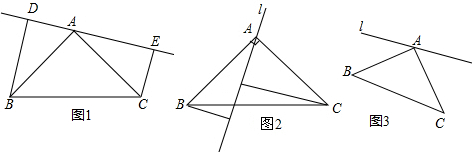
(1)如图1,当D、E两点在直线BC的同侧时,①猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.②若线段BD=a,CE=b.请你求出△ABC的面积(用含a,b的代数式表示);
(2)如图2,当D、E两点在直线BC的两侧时,BD、CE、DE三条线段的数量关系为___;
(3)如图3,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?(直接写出结果即可)

▼优质解答
答案和解析
(1)①∵BD⊥直线l,CE⊥直线l,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
②∵AE=BD,BD=a,
∴AE=a,
在Rt△AEC中,AC2=AE2+CE2=a2+b2,
S△ABC=
AC•AB=
AC2=
(a2+b2).
(2)BD+DE=CE;如图2,
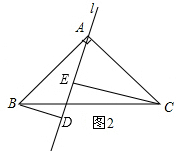
理由如下:
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵BD⊥l,CE⊥l,
∴∠ADB=∠AEC=90°,
∴∠CAD+∠ACE=90°,
∴∠BAD=∠ACE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE+DE=AD,
∴BD+DE=CE.
故答案为:BD+DE=CE.
(3):①当点P在BA上,点Q在AC上,如图3,
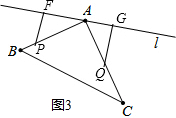
则PB=2t,CQ=3t,AP=22-2t,AQ=28-3t,
∵△PFA与△QAG全等,
∴PA=AQ,即22-2t=28-3t,解得t=6,
即P运动6秒时,△PFA与△QAG全等;
②当点P在AC上,点Q在AB上,如图4,
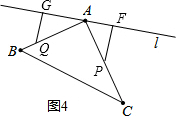
则PA=2t-22,AQ=3t-28,∵△PFA与△QAG全等,
∴PA=AQ,即2t-22=3t-28,解得t=6,舍去;
即P运动6秒时,△PFA与△QAG全等,
当点Q停在点B处,点P在AC上,由PA=QA得2t-22=22,解得t=22,舍去.
综上所述:当t等于6时,△PFA与△QAG全等.
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
|
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
②∵AE=BD,BD=a,
∴AE=a,
在Rt△AEC中,AC2=AE2+CE2=a2+b2,
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)BD+DE=CE;如图2,

理由如下:
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵BD⊥l,CE⊥l,
∴∠ADB=∠AEC=90°,
∴∠CAD+∠ACE=90°,
∴∠BAD=∠ACE,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE+DE=AD,
∴BD+DE=CE.
故答案为:BD+DE=CE.
(3):①当点P在BA上,点Q在AC上,如图3,

则PB=2t,CQ=3t,AP=22-2t,AQ=28-3t,
∵△PFA与△QAG全等,
∴PA=AQ,即22-2t=28-3t,解得t=6,
即P运动6秒时,△PFA与△QAG全等;
②当点P在AC上,点Q在AB上,如图4,

则PA=2t-22,AQ=3t-28,∵△PFA与△QAG全等,
∴PA=AQ,即2t-22=3t-28,解得t=6,舍去;
即P运动6秒时,△PFA与△QAG全等,
当点Q停在点B处,点P在AC上,由PA=QA得2t-22=22,解得t=22,舍去.
综上所述:当t等于6时,△PFA与△QAG全等.
看了如图1,在Rt△ACB中,∠B...的网友还看了以下:
(2009•长宁区二模)手t,曲线C:y=2x(0≤x≤2)两端分别为M、2,且2图⊥x轴于点图. 2020-05-15 …
设直线L分别与X轴Y轴交与点AB,如果直线M:Y=KX+T(T大于0)与直线L平行且交X轴于C,求 2020-06-12 …
已知光滑曲线C:x=x(t),y=y(t),z=z(t)在点(x(t0),y(t0),z(t0)) 2020-07-10 …
一质点作简谐运动,其位移x与时间t关系曲线如图所示,由图可知()A.质点振动的周期是0.9SB.质 2020-07-12 …
一简谐横波沿x轴正向传播,t=0时刻的波形如图(a)所示,x=0.30m处的质点的振动图线如图(b 2020-07-14 …
如图所示甲、乙为一定质量的某种气体的等容或等压变化图象,关于这两个图象的正确说法是()A.甲是等压 2020-07-19 …
一质点做简谐运动,其位移x与时间t的关系曲线如图所示,由图可知()A.质点振动频率是4HzB.t= 2020-07-20 …
一质点做简谐运动,其运动速度与时间的关系曲线如图,最大速度为Vm,t=0时刻,速度v=0.5.若质 2020-08-02 …
如图,四边形AOBC为直角梯形,OC=根号5,OB=5AC,OC所在的直线的解析式为y=2x,平行于 2020-12-05 …
波源S的振动图线如图甲所示,由此产生的简谐波向右传播,已知波上两点S、P相距1.5m,如图乙所示,波 2020-12-15 …