早教吧作业答案频道 -->数学-->
如图1,点M放在正方形ABCD的对角线AC(不与点A重合)上滑动,连结DM,做MN⊥DM交直线AB于N.(1)求证:DM=MN;(2)若将(1)中的正方形变为矩形,其余条件不变(如图2),且DC=2AD,求MD:MN
题目详情
如图1,点M放在正方形ABCD的对角线AC(不与点A重合)上滑动,连结DM,做MN⊥DM交直线AB于N.
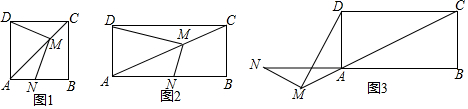
(1)求证:DM=MN;
(2)若将(1)中的正方形变为矩形,其余条件不变(如图2),且DC=2AD,求MD:MN;
(3)在(2)中,若CD=nAD,当M滑动到CA的延长线上时(如图3),请你直接写出MD:MN的比值.

(1)求证:DM=MN;
(2)若将(1)中的正方形变为矩形,其余条件不变(如图2),且DC=2AD,求MD:MN;
(3)在(2)中,若CD=nAD,当M滑动到CA的延长线上时(如图3),请你直接写出MD:MN的比值.
▼优质解答
答案和解析
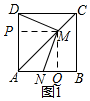 (1)证明:过M作MQ⊥AB于Q,MP⊥AD于P,则∠PMQ=90°,∠MQN=∠MPD=90°,
(1)证明:过M作MQ⊥AB于Q,MP⊥AD于P,则∠PMQ=90°,∠MQN=∠MPD=90°,
∵∠DMN=90°,
∴∠DMP=∠NMQ,
∵ABCD是正方形,
∴AC平分∠DAB,
∴PM=MQ,
在△MDP和△MNQ中,
,
∴△MDP≌△MNQ(ASA),
∴DM=MN;
(2)过M作MS⊥AB于S,MW⊥AD于W,则∠WMS=90°,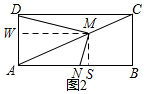
∵MN⊥DM,
∴∠DMW=∠NMS,
又∵∠MSN=∠MWD=90°,
∴△MDW∽MNS,
∴MD:MN=MW:MS=MW:WA,
∵MW∥CD,
∴∠AMW=∠ACD,∠AWM=∠ADC,
∴△AWM∽△ADC,
又∵DC=2AD,
∴MD:MN=MW:WA=CD:DA=2;
(3)MD:MN=n,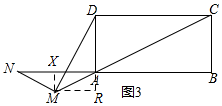
理由:过M作MX⊥AB于X,MR⊥AD于R,则易得△NMX∽△DMR,
∴MD:MN=MR:MX=AX:MX,
由AD∥MX,CD∥AX,易得△AMX∽△CAD,
∴AX:MX=CD:AD,
又∵CD=nAD,
∴MD:MN=CD:AD=n.
 (1)证明:过M作MQ⊥AB于Q,MP⊥AD于P,则∠PMQ=90°,∠MQN=∠MPD=90°,
(1)证明:过M作MQ⊥AB于Q,MP⊥AD于P,则∠PMQ=90°,∠MQN=∠MPD=90°,∵∠DMN=90°,
∴∠DMP=∠NMQ,
∵ABCD是正方形,
∴AC平分∠DAB,
∴PM=MQ,
在△MDP和△MNQ中,
|
∴△MDP≌△MNQ(ASA),
∴DM=MN;
(2)过M作MS⊥AB于S,MW⊥AD于W,则∠WMS=90°,

∵MN⊥DM,
∴∠DMW=∠NMS,
又∵∠MSN=∠MWD=90°,
∴△MDW∽MNS,
∴MD:MN=MW:MS=MW:WA,
∵MW∥CD,
∴∠AMW=∠ACD,∠AWM=∠ADC,
∴△AWM∽△ADC,
又∵DC=2AD,
∴MD:MN=MW:WA=CD:DA=2;
(3)MD:MN=n,

理由:过M作MX⊥AB于X,MR⊥AD于R,则易得△NMX∽△DMR,
∴MD:MN=MR:MX=AX:MX,
由AD∥MX,CD∥AX,易得△AMX∽△CAD,
∴AX:MX=CD:AD,
又∵CD=nAD,
∴MD:MN=CD:AD=n.
看了如图1,点M放在正方形ABCD...的网友还看了以下:
求教工程数学线性代数1若n阶矩阵A为正交矩阵,则A必为可逆矩阵且A-1=A'2若Rank(A)=n 2020-04-12 …
若矩阵A有特征向量i=(10)和j=(01),且它们所对应的特征值分别为λ1=2,λ2=-1.(1 2020-05-14 …
已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交A 2020-06-17 …
已知矩阵A=1121−10(1)若矩阵B=2313−41且3A-X=B,求矩阵X.(2)若矩阵C= 2020-07-15 …
1,设矩阵A=(第一行10-1第二行130第三行021),X为三阶矩阵,且满足矩阵方程AX+I=A 2020-07-18 …
矩形AGFE∽矩形ABCD,AE、AD分别为它们的最短边,点F在AB上,且3AE=2AD.(1)若 2020-07-20 …
(本题满分12分)已知函数(为自然对数的底数).(1)求的最小值;(2)不等式的解集为,若且求实数 2020-08-02 …
相似多边形1.E,F分别是矩形ABCD的边AD,BC的中点,若矩形ABCD与矩形EABF相似,AB 2020-08-03 …
如图1,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF∽矩形ABCO,其相似比为1: 2020-08-03 …
已知A,B为3阶矩阵,且满足2A-1B=B-4E.其中E是3阶单位矩阵;(1)证明:矩阵A-2E可逆 2020-11-03 …