早教吧作业答案频道 -->数学-->
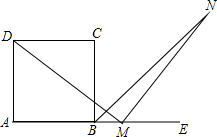
如图,点M为正方形ABCD的边AB(或BA)延长线上任意一点,MN⊥DM且与∠ABC外角的平分线交于点N,此时MD与MN有何数量关系?并加以证明.
题目详情
如图,点M为正方形ABCD的边AB(或BA)延长线上任意一点,MN⊥DM且与∠ABC外角的平分线交于点N,此时MD与MN有何数量关系?并加以证明.

▼优质解答
答案和解析
结论: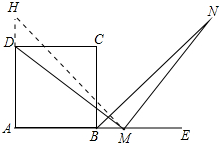 DM=MN.
DM=MN.
证明:延长AD使得DH=BM,
∵四边形ABCD是正方形,
∴AD=AB,∠A=∠ABC=90°,
∴AH=AM,∠H=∠AMH=45°,
∵BN平分∠CBE,∠CBE=90°,
∴∠NBM=∠H=45°,
∵∠NME+∠AMD=90°,∠AMD+∠ADM=90°,
∴∠ADM=∠NME,
∴∠HDM=∠NMB,
在△DHM和△MBN中,
,
∴△DHM≌△MBN,
∴DM=MN.
 DM=MN.
DM=MN.证明:延长AD使得DH=BM,
∵四边形ABCD是正方形,
∴AD=AB,∠A=∠ABC=90°,
∴AH=AM,∠H=∠AMH=45°,
∵BN平分∠CBE,∠CBE=90°,
∴∠NBM=∠H=45°,
∵∠NME+∠AMD=90°,∠AMD+∠ADM=90°,
∴∠ADM=∠NME,
∴∠HDM=∠NMB,
在△DHM和△MBN中,
|
∴△DHM≌△MBN,
∴DM=MN.
看了 如图,点M为正方形ABCD的...的网友还看了以下:
已知二次函数f(x)=a乘x的平方+bx+c(a不等于零)是否存在常数a,b,c,使函数f(x)同 2020-05-22 …
通常,重复保险的分摊方式包括()。A.第一损失方式B.比例责任方式C.限额责任方式D.顺序责任方式E 2020-05-22 …
已知a.b.c是三角形ABC的三遍,且满足a的四次方+b的2次方程c的2次方=b的4次方+a的2次 2020-06-12 …
已知a,b,c均为实数,且a平方+b平方=c平方,且c属于正整数,切当n》2时比较cn次方与an次 2020-07-27 …
一个三位自然数abc的百位,十位,个位上的数字依次为a,b,c,当且仅当a<b且c<b时称为“凸数 2020-07-29 …
已知数列{an}的首项a1=2,且对任意n∈N*,都有an+1=ban+c,其中b,c是常数.(1 2020-07-30 …
高一负数,急!1.设α、β是实系数一元二次方程ax^2+bx+c=0(a≠0)的两个虚根,且(α^ 2020-08-02 …
已知双曲线C:=1(a>0,b>0)的两个焦点分别为F1(-c,0),F2(c,0)(c>0),且c 2020-11-01 …
关于平方根,下列说法正确的是()A.任何一个数有两个平方根,并且他们互为相反数B.负数没有平方根C. 2020-11-06 …
下列说法错误的是A如果一个数有立方根,那么他也一定有平方根B任何一个有理数都有立方根,而且只有一个立 2020-12-07 …