早教吧作业答案频道 -->数学-->
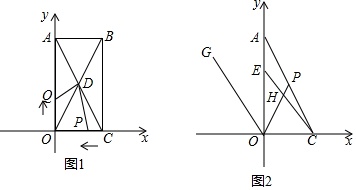
如图,以长方形ABCO中点O为原点,以OC,OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足a-2b+|b-2|=0.(1)求点A,B和C的坐标.(2)已知坐标轴上有两动点P,Q同时出发
题目详情
如图,以长方形ABCO中点O为原点,以OC,OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足
+|b-2|=0.
(1)求点A,B和C的坐标.
(2)已知坐标轴上有两动点P,Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动.Q点从O点出发以2个单位长度每秒的速度沿O→A→B→C的路线移动,点Q到达C点整个运动随之结束.若长方形对角线AC,BO的交点D的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ?若存在,请求出t的值;若不存在,请说明理由;
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,下列两个结论:①
的值不变;②
的值不变,其中有且只有一个结论是正确的,请你找出正确的结论并求其值.
| a-2b |
(1)求点A,B和C的坐标.
(2)已知坐标轴上有两动点P,Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动.Q点从O点出发以2个单位长度每秒的速度沿O→A→B→C的路线移动,点Q到达C点整个运动随之结束.若长方形对角线AC,BO的交点D的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ?若存在,请求出t的值;若不存在,请说明理由;
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,下列两个结论:①
| ∠OHC-∠ACE |
| ∠OEC |
| ∠OHC+∠ACE |
| ∠OEC |

▼优质解答
答案和解析
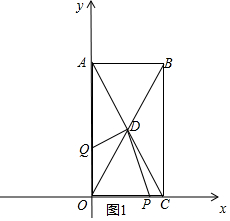 (1)∵
(1)∵
+|b-2|=0,
∴a-2b=0,b-2=0,
解得a=4,b=2,
∴A(0,4),C(2,0),
∵AB∥x轴,BC∥y轴,
∴B(2,4);
(2)由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,
①当0<t≤2时,点Q在线段AO上,
即 CP=t,OP=2-t,OQ=2t,AQ=4-2t,
∴S△DOP=
OP•yD=
(2-t)×2=2-t,
∵S△ODP=S△ODQ,
∴2-t=t,
∴t=1;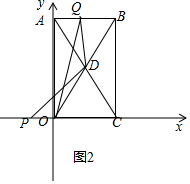
②当2≤t≤3时,点Q在线段AB上,即CP=t,OP=t-2,QB=6-2t,
S△DOP=
OP•yD=
(t-2)×2=t-2,
S△DOP=S△OBQ-S△DBQ=
QB•AO-
QB(yB-yD)=
×(6-2t)×4-
×(6-2t)(4-2)=6-2t,
∵S△DOQ=S△ODQ,
∴t-2=6-2t,
∴t=
;
③当3≤t≤5时,点Q在线段BC上,CP=t,OP=t-2,QB=2t-6,
S△DOP=
OP•yD=
(t-2)×=t-2,
S△DOQ=S△OBQ-S△DBQ=
QB•OC-
QB(xB-xD)=
×(2t-6)-
(6-2t)(2-1)=t-3,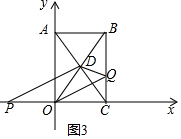
∵S△ODP=S△ODQ,
∴t-2=t-3,无解,
此情况下不存在这样的t,
∴当t=1或t=
时,S△ODP=S△ODQ;
(3)
的值不变,其值为2.
∵∠2+∠3=90°,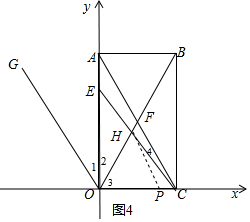
又∵∠1=∠2,∠3=∠FCO,
∴∠GOC+∠ACO=180°,
∴OG∥AC,
∴∠1=∠CAO,
∴∠OEC=∠CAO+∠4=∠1+∠4,
如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,
∴∠PHO=∠GOF=∠1+∠2,
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,
∴
=
=
=2.
 (1)∵
(1)∵| a-2b |
∴a-2b=0,b-2=0,
解得a=4,b=2,
∴A(0,4),C(2,0),
∵AB∥x轴,BC∥y轴,
∴B(2,4);
(2)由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,
①当0<t≤2时,点Q在线段AO上,
即 CP=t,OP=2-t,OQ=2t,AQ=4-2t,
∴S△DOP=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ODP=S△ODQ,
∴2-t=t,
∴t=1;

②当2≤t≤3时,点Q在线段AB上,即CP=t,OP=t-2,QB=6-2t,
S△DOP=
| 1 |
| 2 |
| 1 |
| 2 |
S△DOP=S△OBQ-S△DBQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△DOQ=S△ODQ,
∴t-2=6-2t,
∴t=
| 8 |
| 3 |
③当3≤t≤5时,点Q在线段BC上,CP=t,OP=t-2,QB=2t-6,
S△DOP=
| 1 |
| 2 |
| 1 |
| 2 |
S△DOQ=S△OBQ-S△DBQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

∵S△ODP=S△ODQ,
∴t-2=t-3,无解,
此情况下不存在这样的t,
∴当t=1或t=
| 8 |
| 3 |
(3)
| ∠OHC+∠ACE |
| ∠OEC |
∵∠2+∠3=90°,

又∵∠1=∠2,∠3=∠FCO,
∴∠GOC+∠ACO=180°,
∴OG∥AC,
∴∠1=∠CAO,
∴∠OEC=∠CAO+∠4=∠1+∠4,
如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,
∴∠PHO=∠GOF=∠1+∠2,
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,
∴
| ∠OHC+∠ACE |
| ∠OEC |
| ∠1+∠2+∠4+∠4 |
| ∠1+∠4 |
| 2(∠1+∠4) |
| ∠1+∠4 |
看了如图,以长方形ABCO中点O为...的网友还看了以下:
如图,在平面直角坐标系中,已知直线m经过点(3,0)且与x轴垂直,点A为其上一动点,直线l:y=1 2020-05-13 …
经过点P(a,b)且垂直于x轴(平行于y轴)的直线可表示为经过点P(a,b)且垂直于y轴(平行于x 2020-05-23 …
初三数学直线y=-2x+8分别与x轴,y轴相交于点a,b.o点为原点.a点坐标为(4,0)若p为y 2020-06-14 …
在平面直角坐标系中,直线L1:y=2x+b交x轴正半轴于点A,点B(4,0)在点A的右边,现过点B 2020-06-14 …
如图,在平面直角坐标系中有两点A(2,0)和B(0,2),a为过点A且垂直于x轴的直线,P(x,0 2020-06-15 …
在平面直角坐标系中,A(0,2),B(0,3),过点B作直线l平行x轴,p(a,3)是直线l上的动 2020-07-30 …
为什么倾斜角为90°就说直线没有斜率,而倾斜角为0°就说斜率为0?90°的时候不是直线垂直于x轴, 2020-07-31 …
点P、Q在反比例函数y=x分之k(k大于0)第一象限内的图像上,过点P作PE垂直于y轴,过点Q作Q 2020-08-01 …
(2009•泰兴市模拟)已知:如图1所示,直线x+y=9与x轴、y轴相交于C、D两点,直线2x+3y 2020-12-18 …
在直角坐标系中,如果a是正数,b是负数,则点(0,a),(b,0)分别在什么位置上?但是点(0,a) 2021-02-04 …