早教吧作业答案频道 -->数学-->
如图是二次函数y=ax2+bx=c的图象,则a、b、c满足()A、a>0,b>0,c>0B、a>0,b<0,c>0C、a>0,b>0,c<0D、a>0,b<0,c<0
题目详情
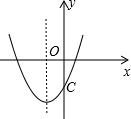 如图是二次函数y=ax 2 +bx=c的图象,则a、b、c满足( )
如图是二次函数y=ax 2 +bx=c的图象,则a、b、c满足( )| A、a>0,b>0,c>0 |
| B、a>0,b<0,c>0 |
| C、a>0,b>0,c<0 |
| D、a>0,b<0,c<0 |
▼优质解答
答案和解析
考点:
二次函数图象与系数的关系
专题:
计算题
分析:
根据抛物线开口方向确定a的符号;根据抛物线的对称轴的位置得到a、b同号,则b>0;根据抛物线与y轴的交点位置确定c的符号.
∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴的左侧,∴a、b同号,∴b>0,∵抛物线与y轴交点在x轴下方,∴c<0.故选C.
点评:
本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);△决定抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
考点:
二次函数图象与系数的关系
专题:
计算题
分析:
根据抛物线开口方向确定a的符号;根据抛物线的对称轴的位置得到a、b同号,则b>0;根据抛物线与y轴的交点位置确定c的符号.
∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴的左侧,∴a、b同号,∴b>0,∵抛物线与y轴交点在x轴下方,∴c<0.故选C.
点评:
本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);△决定抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
看了如图是二次函数y=ax2+bx...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
因式分解a3(b-c)+b3(c-a)+c3(a-b)如果用待定系数法解,得a3(b-c)+b3( 2020-05-16 …
一元二次方程 -若c(c不等于0)为关于x的一元二次方程x²+bx+c=0的根,则c+b的值为( 2020-05-16 …
分解因式(a-b-c)(a+b-c)-(b-c-a)(b+c-a)正确答案是这个:(a+b-c)( 2020-05-17 …
分式方程请观察下列方程和它们的根请观察下列方程和它们的根:x+1/x=c+1/c的解是x=c或x= 2020-06-06 …
关于x的方程x+1/x=c+1/c的解是x1=c,x2=1/c;x-1/x=c-c/1(即x+(- 2020-07-21 …
用C(A)表示非空集合A中的元素个数,定义A*B=C(A)-C(B),当C(A)≥C(B)C(B) 2020-07-22 …
用C(A)表示非空集合A中的元素个数,定义A*B=C(A)-C(B),当C(A)≥C(B)C(B) 2020-07-22 …
直接写口数c.6÷c.6=6.3×c.四=12.五×c.8=1c÷c.五=c.8÷c.c4=c.42 2020-10-31 …
已知函数f(x)=ax^2+bx+c(c≠0),满足f(-1)=f(3)=0,且f(0)=6,求f( 2020-12-08 …