如图，抛物线y=ax2+bx+c经过点（-1，0），与x轴的另一个交点在点（2，0）和点（3，0）之间，与y轴相交于正半轴：①b=a+c；②a+b>0；③2a+b>0；④b2-4ac4a+a+b+c<0中，正确结论的个数是（

Question

如图，抛物线y=ax²+bx+c经过点（-1，0），与x轴的另一个交点在点（2，0）和点（3，0）之间，与y轴相交于正半轴：①b=a+c；②a+b>0；③2a+b>0；④

(b2-4ac)/(4a)+a+b+c<0中，正确结论的个数是（　　）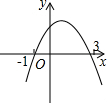

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

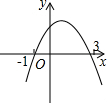①把点（-1，0）代入抛物线y=ax²+bx+c，得到：a-b+c=0，则b=a+c；故①正确；

②如图所示，抛物线开口方向向下，则a<0．
∵抛物线y=ax²+bx+c经过点（-1，0），另一个交点在点（2，0）和点（3，0）之间，
∴11+x₂=-(b)/(a)<2，
即1+(b)/(a)<0，(a+b)/(a)<0，
∴a+b>0．
故②正确；

③∴对称轴为直线0<-(b)/(2a)<1，
∴b<-2a，
∴b+2a<0．
故③错误；

④由抛物线的顶点坐标可以判定(b2-4ac)/(4a)>0．
当x=1时，y>0，即a+b+c>0，
∴(b2-4ac)/(4a)+a+b+c>0，
故④错误；
综上所述，正确的个数是2个，
故选：B．