早教吧作业答案频道 -->数学-->
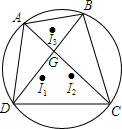
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
题目详情
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.

▼优质解答
答案和解析
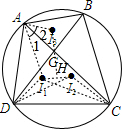 证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,
证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,
延长I3G交I1I2于点H,
∵I1、I2、I3分别为△ADC、△BDC、△ABG的内心,
∴∠AI3G=90°+
∠ABD,∠AI1C=90°+
∠ADC,
∴∠DI1C=90°+
∠DAC,∴∠DI2C=90°+
∠DBC,
∠1+∠2=
(∠DAC+∠BAC),
又∵∠DAC=∠DBC,
∴∠DI1C=∠DI2C,
∴点D、I1、I2、C四点共圆,
∴∠I2I1C=∠I2DC=
∠BDC=
∠BAC,
∴∠I3HI1=360°-(∠1+∠2+∠AI3G+∠AI1H)
∵∠1+∠2+∠AI3G+∠AI1H=
(∠DAC+∠BAC)+90°+
∠ABD+90°+
∠ADC-I2I1C
=180°+
(∠DAC+∠BAC+∠ABD+∠ADC+∠BAC)
=180°+
(∠ABD+∠DBC+∠ADC)
=270°,
∴∠I3HI1=360°-270°=90°,
∴I3G⊥I1I2.
 证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,
证明:分别连接AI3,AI1,DI1,DI2,CI1,CI2,延长I3G交I1I2于点H,
∵I1、I2、I3分别为△ADC、△BDC、△ABG的内心,
∴∠AI3G=90°+
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DI1C=90°+
| 1 |
| 2 |
| 1 |
| 2 |
∠1+∠2=
| 1 |
| 2 |
又∵∠DAC=∠DBC,
∴∠DI1C=∠DI2C,
∴点D、I1、I2、C四点共圆,
∴∠I2I1C=∠I2DC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠I3HI1=360°-(∠1+∠2+∠AI3G+∠AI1H)
∵∠1+∠2+∠AI3G+∠AI1H=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=180°+
| 1 |
| 2 |
=180°+
| 1 |
| 2 |
=270°,
∴∠I3HI1=360°-270°=90°,
∴I3G⊥I1I2.
看了如图,四边形ABCD内接于圆,...的网友还看了以下:
设A,B,A+B均为n阶可逆矩阵,则(A-1+B-1)-1=() A.A-1+BB.A+B C.B 2020-04-05 …
1.若正数a,b满足ab-(a+b)=1,则a+b最小值为多少?2.设M=(1/a-1)(1/b- 2020-04-05 …
若n阶方阵A与B满足AB+A+B=E(E为单位矩阵).证明(1)B+E为可逆矩阵(2)(B+E)^ 2020-04-05 …
概率题急求解1设A,B为随机事件且P(A)=0.7,P(A-B)=0.3,求P(A非B非).2设A 2020-04-12 …
在平面直角坐标系中,对于平面内任何一点(a,b),若规定以下三种变换:①f(a,b)=(-a,b) 2020-04-26 …
在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:1f(a,b)=(-a,b). 2020-04-26 …
已知a,b>0,且a+b=1,求证a分1+b分1大于等于4因为 a>0,b>0 且a+b=1所以 2020-05-15 …
已知a+0.1=b-1,则a()b已知a-0.1=b+1,则a()b已知a*0.1=b/10,则a 2020-05-17 …
已知f(X)=Lg1-X/1+X,a,b属于(-1,1)求证:f(a)+f(B)=F(A+B)/1 2020-05-22 …
数学几道计算题、5x(2x+4)+x(x-1)x(x-3)-2x^2(x+1),x=3a(b-c) 2020-06-06 …