早教吧作业答案频道 -->数学-->
如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.(I)求证:四边形ABCD为平行四边形;(II)若E,F分别为AB1,D1C1上的点,AB1=CC1=2BB1=4,AE=D1F=1.(i)求证:CD丄平面DEF;(
题目详情
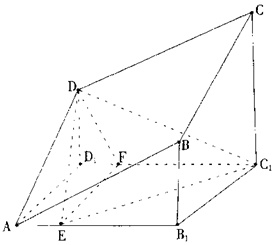
如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.
(I)求证:四边形ABCD为平行四边形;
(II)若E,F分别为AB1,D1C1上的点,AB1=CC1=2BB1=4,AE=D1F=1.
(i)求证:CD丄平面DEF;
(ii)求二面角D-EC1-D1的余弦值.
(I)求证:四边形ABCD为平行四边形;
(II)若E,F分别为AB1,D1C1上的点,AB1=CC1=2BB1=4,AE=D1F=1.
(i)求证:CD丄平面DEF;
(ii)求二面角D-EC1-D1的余弦值.

▼优质解答
答案和解析
证明:(Ⅰ)∵BB1⊥面ABCD,CC1⊥面ABCD,
∴BB1∥CC1,又AB1∥D1C1,AB1,BB1是面ABB1内两相交直线,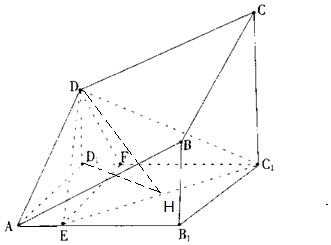
D1C1,CC1是面CC1,D1D内两相交直线,
∴面ABB1∥面CC1D1D,
同理,面ADD1∥面BB1C1C,
∵A、B、C、D四点共面,故AB∥CD,BC∥AD,
∴四边形ABCD为平行四边形.
(Ⅱ)(i)由题意,EF⊥平面CC1D1D,∴EF⊥CD,
∵AD=BC,AB1=CC1=2BB1=4,AE=D1F=1.
∴DD1=2,DF=
,CF=5,CD=AB=2
,
∴DF2+DC2=FC2,∴CD⊥DF,
∵CD⊥EF,DF∩EF=F,∴CD⊥平面DEF.
(ii)过点D1作D1H⊥EC1于点H,连结DH,
∵DD1⊥平面AB1C1D1,故DH⊥EC1,
∴∠DHD1是二面角D-EC1-D1的平面角,
在正方形AB1C1D1中,sin∠D1C1E=
,
D1H=D1C1,•sin∠D1C1E=4×
=
,
在Rt△DD1H中,∵DD1=2,∴tan∠DHD1=
,
∴cos∠DHD1=
,
∴二面角D-EC1-D1的余弦值为
.
∴BB1∥CC1,又AB1∥D1C1,AB1,BB1是面ABB1内两相交直线,

D1C1,CC1是面CC1,D1D内两相交直线,
∴面ABB1∥面CC1D1D,
同理,面ADD1∥面BB1C1C,
∵A、B、C、D四点共面,故AB∥CD,BC∥AD,
∴四边形ABCD为平行四边形.
(Ⅱ)(i)由题意,EF⊥平面CC1D1D,∴EF⊥CD,
∵AD=BC,AB1=CC1=2BB1=4,AE=D1F=1.
∴DD1=2,DF=
| 5 |
| 5 |
∴DF2+DC2=FC2,∴CD⊥DF,
∵CD⊥EF,DF∩EF=F,∴CD⊥平面DEF.
(ii)过点D1作D1H⊥EC1于点H,连结DH,
∵DD1⊥平面AB1C1D1,故DH⊥EC1,
∴∠DHD1是二面角D-EC1-D1的平面角,
在正方形AB1C1D1中,sin∠D1C1E=
| 4 |
| 5 |
D1H=D1C1,•sin∠D1C1E=4×
| 4 |
| 5 |
| 16 |
| 5 |
在Rt△DD1H中,∵DD1=2,∴tan∠DHD1=
| 5 |
| 8 |
∴cos∠DHD1=
8
| ||
| 89 |
∴二面角D-EC1-D1的余弦值为
8
| ||
| 89 |
看了如图BB1,CC1,DD1均垂...的网友还看了以下:
配有一个梯形的图(它有4条边,4个角,是一个四形,这种说法对吗)配有图形是个梯形(问它有4条边,4个 2020-03-31 …
数学直线与平面关系问题长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,求BC1与平 2020-05-13 …
已知Rt△ABC的周长是4+4根号3,斜边上的中线长是2,则S△ABC=?设两条直角边为x、y.因 2020-05-14 …
已知直角三角形的高为1.3米,底边为4.5米,求斜边?拜托了各位谢谢高1.3米,底边4.5米,求斜 2020-05-22 …
给小昆虫排队.(1)一共有只昆虫.(2)从右边数,青蛙是第个,第3个是.(3)从左边数,蜗牛是第个 2020-06-16 …
有8张卡片,每张卡片上写有一个数字,左边4张卡片上分别写着2、4、5、7,右边4张卡片上分别写着1 2020-07-13 …
n条边围成凸n边形的充要条件是什么三条边围成三角形的充要条件是两边之和大于第三边,4条边围成凸4边 2020-07-13 …
几何三角形如已知三角形的对边A为3临边B为4时怎么算出临边与斜边的夹角度数是直角三角形A边是对边为 2020-07-30 …
急:用对数换底公式化简logaC乘以logcAlog左下角2右边3乘以log左下角3右边4乘以lo 2020-08-01 …
GPS点已经在现场不好了,外业测量时先测那个点和后侧那个点有没有什么影响.假如我有1对基点,间隔为4 2021-01-25 …