早教吧作业答案频道 -->数学-->
如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.(1)求证:AM=AD+MC;(2)AM=DE+BM是否成立?请直接做出判断,不需要证明.
题目详情
如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.
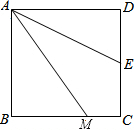
(1)求证:AM=AD+MC;
(2)AM=DE+BM是否成立?请直接做出判断,不需要证明.

(1)求证:AM=AD+MC;
(2)AM=DE+BM是否成立?请直接做出判断,不需要证明.
▼优质解答
答案和解析
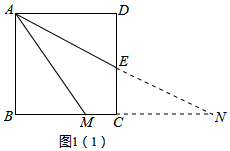 (1)证明:延长AE、BC交于点N,如图1(1),
(1)证明:延长AE、BC交于点N,如图1(1),
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴MA=MN,
在△ADE和△NCE中,
,
∴△ADE≌△NCE(AAS),
∴AD=NC,
∴MA=MN=NC+MC=AD+MC;
(2) AM=DE+BM成立,
理由如下:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.
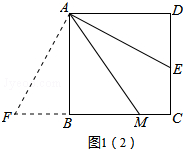 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC,
∵AF⊥AE,
∴∠FAE=90°,
∴∠FAB=90°-∠BAE=∠DAE,
在△ABF和△ADE中,
,
∴△ABF≌△ADE(ASA),
∴BF=DE,∠F=∠AED,
∵AB∥DC,
∴∠AED=∠BAE,
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM,
∴∠F=∠FAM,
∴AM=FM,
∴AM=FB+BM=DE+BM.
 (1)证明:延长AE、BC交于点N,如图1(1),
(1)证明:延长AE、BC交于点N,如图1(1),∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴MA=MN,
在△ADE和△NCE中,
|
∴△ADE≌△NCE(AAS),
∴AD=NC,
∴MA=MN=NC+MC=AD+MC;
(2) AM=DE+BM成立,
理由如下:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.
 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC,
∵AF⊥AE,
∴∠FAE=90°,
∴∠FAB=90°-∠BAE=∠DAE,
在△ABF和△ADE中,
|
∴△ABF≌△ADE(ASA),
∴BF=DE,∠F=∠AED,
∵AB∥DC,
∴∠AED=∠BAE,
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM,
∴∠F=∠FAM,
∴AM=FM,
∴AM=FB+BM=DE+BM.
看了如图,已知四边形ABCD是正方...的网友还看了以下:
The new supermarket is ----- for18 hours A:open B 2020-05-14 …
-You are going out today,aren't you?--__,I want t 2020-05-16 …
-_______ either she or you to go and attend the…- 2020-05-16 …
请见谅)甲,乙两人加工某种零件,甲比乙每天多做a个,甲做m个零件的天数与乙做n个零件所用的天数相等 2020-06-23 …
价格为a元的甲糖m千克与价格为b元的乙糖n千克混合出售,则每千克的售价为()A.a+b2元B.(a 2020-07-08 …
如图,平行四边形ABCD中,M为DC中点,N为BC中点,设向量AB=b,向量AD=d,向量AM=m 2020-07-22 …
在化学反应aM+bN=cP+dQ中,10gaM与6gbN恰好完全反应,其中生成2gcP,若要生成7g 2020-10-30 …
急.初中的几何题△ABC中,AM是BC上的中线,在AM上取一点P,连结BP和CP并分别延长与AC交与 2020-11-02 …
一、能证明的证明,不能的举反例哦!1、如果a>b,判断a-c与b-c的大小2、如果a>b,cb,c> 2020-11-27 …
已知在正△ABC中,AB=4,点M是射线AB上的任意一点(点M与点A、B不重合),点N在边BC的延长 2021-01-12 …