早教吧作业答案频道 -->数学-->
二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(-1,0)、B(4,0)(1)求此二次函数的表达式(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(-76,0),动
题目详情
二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(-1,0)、B(4,0)
(1)求此二次函数的表达式
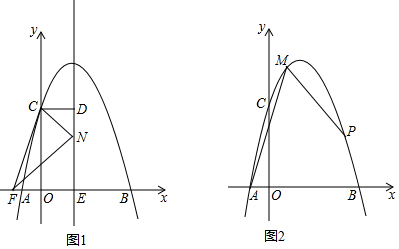
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(-
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标.
(1)求此二次函数的表达式
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(-
| 7 |
| 6 |
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标.

▼优质解答
答案和解析
(1)当x=0时,y=4,
∴C(0,4).
设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入得:-4a=4,解得a=-1,
∴抛物线的解析式为y=-x2+3x+4.
(2)x=-
=
.
∴CD=
,EF=
.
设点N的坐标为(0,a)则ND=4-a,NE=a.
当△CDN∽△FEN时,
=
,即
=
,解得a=
,
∴点N的坐标为(0,
).
当△CDN∽△NEF时,
=
,即
=
,解得:a=2.
∴点N的坐标为(0,2).
综上所述,点N的坐标为(0,
)或(0,2).
(3)如图所示:过点A作AD∥y轴,过点M作DM∥x轴,交点为D,过点A作AE⊥AM,取AE=AM,作EF⊥x轴,垂足为F,连结EM交抛物线与点P.
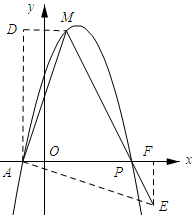
∵AM=AE,∠MAE=90°,
∴∠AMP=45°.
将x=1代入抛物线的解析式得:y=6,
∴点M的坐标为(1,6).
∴MD=2,AD=6.
∵∠DAM+∠MAF=90°,∠MAF+∠FAE=90°,
∴∠DAM=∠FAE.
在△ADM和△AFE中,
,
∴△ADM≌△AFE.
∴EF=DM=2,AF=AD=6.
∴E(5,-2).
设EM的解析式为y=kx+b.
将点M和点E的坐标代入得:
,解得k=-2,b=8,
∴直线EM的解析式为y=-2x+8.
将y=-2x+8与y=-x2+3x+4联立,解得:x=1或x=4.
将x=4代入y=-2x+8得:y=0.
∴点P的坐标为(4,0).
∴C(0,4).
设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入得:-4a=4,解得a=-1,
∴抛物线的解析式为y=-x2+3x+4.
(2)x=-
| b |
| 2a |
| 3 |
| 2 |
∴CD=
| 3 |
| 2 |
| 8 |
| 3 |
设点N的坐标为(0,a)则ND=4-a,NE=a.
当△CDN∽△FEN时,
| EM |
| DN |
| EF |
| CD |
| a |
| 4-a |
| ′16 |
| 9 |
| 64 |
| 25 |
∴点N的坐标为(0,
| 64 |
| 25 |
当△CDN∽△NEF时,
| CD |
| NE |
| DN |
| EF |
| ||
| a |
| 4-a | ||
|
∴点N的坐标为(0,2).
综上所述,点N的坐标为(0,
| 64 |
| 25 |
(3)如图所示:过点A作AD∥y轴,过点M作DM∥x轴,交点为D,过点A作AE⊥AM,取AE=AM,作EF⊥x轴,垂足为F,连结EM交抛物线与点P.

∵AM=AE,∠MAE=90°,
∴∠AMP=45°.
将x=1代入抛物线的解析式得:y=6,
∴点M的坐标为(1,6).
∴MD=2,AD=6.
∵∠DAM+∠MAF=90°,∠MAF+∠FAE=90°,
∴∠DAM=∠FAE.
在△ADM和△AFE中,
|
∴△ADM≌△AFE.
∴EF=DM=2,AF=AD=6.
∴E(5,-2).
设EM的解析式为y=kx+b.
将点M和点E的坐标代入得:
|
∴直线EM的解析式为y=-2x+8.
将y=-2x+8与y=-x2+3x+4联立,解得:x=1或x=4.
将x=4代入y=-2x+8得:y=0.
∴点P的坐标为(4,0).
看了二次函数y=ax2+bx+4的...的网友还看了以下:
高中数学题,有关椭圆的已知椭圆C:y^2/a^2+x^2/b^2=1(a>b>0)的两焦点与短轴的 2020-05-13 …
高一函数中映射的问题已知集合A={x,y},B={0,1}.构造从集合A到集合B的映射,试问能构造 2020-05-22 …
直线L1:2x-y+b=0与直线L2:3x-y-4=0的交点在x轴上,求b的值. 2020-06-27 …
直线l1:3x-y+4=0与直线l2:2x-y+b=0的交点在y轴上,求b的值. 2020-06-27 …
设直线l1:ax-by+4=0,l2:(a-1)x+y+b=0,求满足下列条件的a,b的值.(1) 2020-07-12 …
matlab解方程组问题S=solve('b-a=0.72','c+0.5*b-1.5*a=50' 2020-07-23 …
已知点P(x0,y0)和直线kx-y+b=0(由y=kx+b变形而得),则点P到直线kx-y+b=0 2020-11-03 …
高二数学已知函数y=(2x^2+ax+b)/(x^2+1)的值域为[1,3],求a、b的值.先把原函 2020-11-18 …
已知椭圆x^2/a^2+y^2/b^2=1(a>0,b>0)的离心率e=√6/3,右焦点F到直线x/ 2020-12-05 …
高一数学集合题.设A={y|y=x2+2x+a,x∈R},B={x|3-x≤0},若A包含于B,则实 2020-12-07 …