早教吧作业答案频道 -->数学-->
数列{an}是等差数列,Sn是其前n项和(n∈N*),若.(1)求数列{an}的通项公式;(2)设,Tn是数列{bn}的前n项和,求Tn的表达式;(3)设,求C2+C4+C6+…+C2n+2.
题目详情
数列{a n }是等差数列,S n 是其前n项和(n∈N * ),若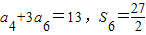 .
.
(1)求数列{a n }的通项公式;
(2)设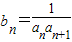 ,T n 是数列{b n }的前n项和,求T n 的表达式;
,T n 是数列{b n }的前n项和,求T n 的表达式;
(3)设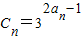 ,求C 2 +C 4 +C 6 +…+C 2n+2 .
,求C 2 +C 4 +C 6 +…+C 2n+2 .
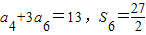 .
.(1)求数列{a n }的通项公式;
(2)设
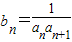 ,T n 是数列{b n }的前n项和,求T n 的表达式;
,T n 是数列{b n }的前n项和,求T n 的表达式;(3)设
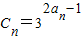 ,求C 2 +C 4 +C 6 +…+C 2n+2 .
,求C 2 +C 4 +C 6 +…+C 2n+2 .▼优质解答
答案和解析
分析:
(1)直接把条件转化为首项和公差来表示,求出首项和公差,即可求出数列{an}的通项公式;(2)直接把上一问的结果代入,求出数列{bn}的通项公式;再利用裂项相消法求出Tn的表达式;(3)先把所求数列{an}的通项公式代入求出=3n,进而得到c2,c4,c6…c2n-2是首项为9,公比为9的等比数列.再代入等比数列的求和公式即可求C2+C4+C6+…+C2n+2.
(1)由已知得:解得:.所以an=1+(n-1)×=.(2)∵==4()∴sn=4[()+()+…+()]=4(-)=.(3)∵=3n,∴c2,c4,c6…c2n-2是首项为9,公比为9的等比数列.∴C2+C4+C6+…+C2n+2=32+34+…+32n+2==.
点评:
本题主要考查等差数列和等比数列的综合问题.解决本题的关键在于求出数列{an}的通项公式以及裂项相消求和的运用.
分析:
(1)直接把条件转化为首项和公差来表示,求出首项和公差,即可求出数列{an}的通项公式;(2)直接把上一问的结果代入,求出数列{bn}的通项公式;再利用裂项相消法求出Tn的表达式;(3)先把所求数列{an}的通项公式代入求出=3n,进而得到c2,c4,c6…c2n-2是首项为9,公比为9的等比数列.再代入等比数列的求和公式即可求C2+C4+C6+…+C2n+2.
(1)由已知得:解得:.所以an=1+(n-1)×=.(2)∵==4()∴sn=4[()+()+…+()]=4(-)=.(3)∵=3n,∴c2,c4,c6…c2n-2是首项为9,公比为9的等比数列.∴C2+C4+C6+…+C2n+2=32+34+…+32n+2==.
点评:
本题主要考查等差数列和等比数列的综合问题.解决本题的关键在于求出数列{an}的通项公式以及裂项相消求和的运用.
看了数列{an}是等差数列,Sn是...的网友还看了以下:
在等差数列{an}中:(1)已知a5+a10=58,a4+a9=50,求S10;(2)已知S7=4 2020-05-14 …
n边形的每一个内角都相等,它的一个外角等于正十边形的一个内角的512.(1)求正十边形的内角和;( 2020-05-20 …
已知等比数列{an}满足a3=12,a8=38,记其前n项和为Sn.(1)求数列{an}的通项公式 2020-05-23 …
n边形的每一个内角都相等,它的一个外角等于正十边形的一个内角的512.(1)求正十边形的内角和;( 2020-06-17 …
已知Sn为等差数列{an}的前n项和,a4=9,a9=-6,Sn=63,求n. 2020-07-09 …
已知等差数列{an}的前n项和为Sn,且满足S13=104,公差d∈N*.(1)若a2,a5,a1 2020-07-17 …
(1)已知C153x-2=C15x+1,求x的值.(2)若(3x-1x)n(n∈N)的展开式中第3 2020-07-18 …
等差数列中{an}中,a10=30,a20=50;(1)求a1,d;(2)求通项公式an;(3)若 2020-07-19 …
等差数列{an}中,已知a10=30,a20=50,前n项和记为Sn.(1)求通项an;(2)若S 2020-07-19 …
已知等差数列{an},a1+a2+a3+a4=40,an+an-1+an-2+an-3=80,Sn= 2020-10-31 …