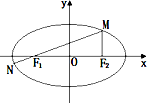
设F1，F2分别是椭圆C：x2a2+y2b2=1(a>b>0)的左右焦点，M是椭圆C上一点，且直线MF2与x轴垂直，直线MF1与C的另一个交点为N．（1）若直线MN的斜率为34，求C的离心率；（2）若直线MN在y轴上的截

Question

设F₁，F₂分别是椭圆C：(x2)/(a2)+(y2)/(b2)=1(a>b>0)的左右焦点，M是椭圆C上一点，且直线MF₂与x轴垂直，直线MF₁与C的另一个交点为N．

（1）若直线MN的斜率为(3)/(4)，求C的离心率；
（2）若直线MN在y轴上的截距为2，且MN=5F₁N，求椭圆C的方程．

Answer 1

（1）椭圆C：(x2)/(a2)+(y2)/(b2)=1(a>b>0)的左右焦点F₁（-c，0），F₂（c，0），
由直线MF₂与x轴垂直，则M(c，(b2)/(a))，
则kMN=kF1M=((b2)/(a))/(2c)=(3)/(4)⇒2b2=3ac，
2a²-2c²=3ac，
由e=(c)/(a)，同时除以a²，整理得：2e²+3e-2=0，解得：e=(1)/(2)，或e=-2（舍去），
∴C的离心率(1)/(2)；（5分）
（2）记直线MN与y轴的交点为D（0，2），则丨MF₂丨=4，即(b2)/(a)=4①，
∵丨MN丨=5丨F₁N丨，
∴

DF1

=2

F1N

，则N（-(3c)/(2)，-1），
将N的坐标代入椭圆方程得(9c2)/(4a2)+(1)/(b2)=1②
由①②及c²=a²-b²得a²=49，b²=28，
故所求椭圆C的方程为(x2)/(49)+(y2)/(28)=1．                               （12分）