早教吧作业答案频道 -->数学-->
如图,三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.(1)证明:平面AEF⊥平面ACC1A1;(2)若AA1=3,求点E到平面ACF的距离.
题目详情
如图,三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.
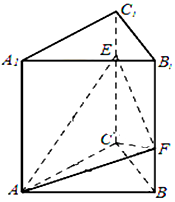
(1)证明:平面AEF⊥平面ACC1A1;
(2)若AA1=3,求点E到平面ACF的距离.

(1)证明:平面AEF⊥平面ACC1A1;
(2)若AA1=3,求点E到平面ACF的距离.
▼优质解答
答案和解析
证明:(1)取AC中点M,连接BM,则BM⊥AC,因为AA1⊥底面ABC,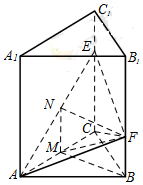
所以侧面ACC1A1⊥底面ABC,所以BM⊥平面ACC1A1.
取AE中点N,连接MN,FN,则MN∥EC,且MN=
EC,
又因为BB1∥CC1,EC=2FB,所以FB∥EC且FB=
EC,
所以MN∥FB且MN=FB,所以四边形BMNF是平行四边形,
所以FN∥BM,所以FN⊥平面ACC1A1.又FN⊂平面AEF,
所以平面AEF⊥平面ACC1A1. …(6分)
(2)由(1)可知,FN⊥平面ACE,连接MF,由AC⊥平面BMNF得AC⊥MF,
因为AA1=3,依题意得MF=
=2,所以S△ACF=
×2×2=2,
设点E到平面ACF的距离为h,由VE-ACF=VF-ACE,得
S△ACF•h=
S△ACE•FN,
即2h=
×2×2×
,所以h=
故点E到平面ACF的距离为
. …(12分)

所以侧面ACC1A1⊥底面ABC,所以BM⊥平面ACC1A1.
取AE中点N,连接MN,FN,则MN∥EC,且MN=
| 1 |
| 2 |
又因为BB1∥CC1,EC=2FB,所以FB∥EC且FB=
| 1 |
| 2 |
所以MN∥FB且MN=FB,所以四边形BMNF是平行四边形,
所以FN∥BM,所以FN⊥平面ACC1A1.又FN⊂平面AEF,
所以平面AEF⊥平面ACC1A1. …(6分)
(2)由(1)可知,FN⊥平面ACE,连接MF,由AC⊥平面BMNF得AC⊥MF,
因为AA1=3,依题意得MF=
(
|
| 1 |
| 2 |
设点E到平面ACF的距离为h,由VE-ACF=VF-ACE,得
| 1 |
| 3 |
| 1 |
| 3 |
即2h=
| 1 |
| 2 |
| 3 |
| 3 |
故点E到平面ACF的距离为
| 3 |
看了如图,三棱柱ABC-A1B1C...的网友还看了以下:
1.判断a、b、c能否构成三角形的三条边长的条件是().选项:a、a>0&&b>0&&c>0b、a+ 2020-03-31 …
求证在三角形ABC和A'B'C'中,角A=角A',角B=B',AC+BC=A'C'+B'C',那么 2020-05-23 …
正余弦综合应用1.在三角形ABC中,a,b,c分别为三个内角A,B,C所对的边,两个向量P=(a+ 2020-06-03 …
已知下列命题:1在△ABC中∠A=∠C-∠B则△ABC为直角三角形2在△ABC中若∠A:∠B:∠C 2020-07-04 …
急求~~1,在三角形ABC中,a平方+b平方+c平方sinC=2倍根号三乘absinC,判i断三角 2020-07-14 …
如果三条线段的长a,b,c满足b/a=c/b=√5-1/2,那么a,b,c称中为“黄金线段组”,黄 2020-07-17 …
1.若平行四边形ABCD相似于平行四边形A'B'C'D',平行四边形ABCE的面积:平行四边形A' 2020-08-01 …
已知a,b,c,d为正数,a>b>c>d,记x=√(ab+cd)(a-b)(c-d),y=√(ac+ 2020-11-03 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
如图,图中的四边形都是正方形,三角形都是直角三角形,其中正方形的面积分别记为A、B、C、D,则它们之 2021-01-22 …