若偶函数y=f（x），x∈R，满足f（x+2）=-f（x），且x∈[0，2]时，f（x）=1-12x，则方程f（x）=log8|x|在[-10，10]内的根的个数为（）A.12B.10C.9D.8

Question

若偶函数y=f（x），x∈R，满足f（x+2）=-f（x），且x∈[0，2]时，f（x）=1-

(1)/(2)x，则方程f（x）=log₈|x|在[-10，10]内的根的个数为（　　）

A. 12

B. 10

C. 9

D. 8

Answer 1

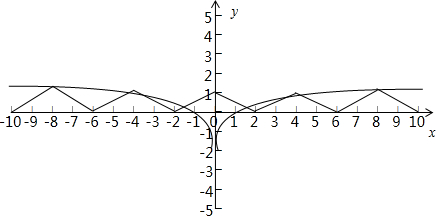∵函数y=f（x）为
偶函数，且满足f（x+2）=-f（x），
∴f（x+4）=f（x+2+2）=-f（x+2）=f（x），
∴偶函数y=f（x）
为周期为4的函数，
由x∈[0，2]时，
f（x）=1-(1)/(2)x，可作出函数f（x）在[-10，10]的图象，
同时作出函数f（x）=log₈|x|在[-10，10]的图象，交点个数即为所求．
数形结合可得交点个为8，
故选：D．