早教吧作业答案频道 -->数学-->
已知函数f(x)=log3x-1x+1,g(x)=-2ax+a+1,h(x)=f(x)+g(x).(Ⅰ)当a=-1时,证明h(x)是奇函数;(Ⅱ)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
题目详情
已知函数f(x)=log3
,g(x)=-2ax+a+1,h(x)=f(x)+g(x).
(Ⅰ)当a=-1时,证明h(x)是奇函数;
(Ⅱ)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
| x-1 |
| x+1 |
(Ⅰ)当a=-1时,证明h(x)是奇函数;
(Ⅱ)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
▼优质解答
答案和解析
 (Ⅰ)证明:当a=-1时,
(Ⅰ)证明:当a=-1时,
f(x)=log3
,g(x)=2x,
h(x)=log3
+2x,
定义域为(-∞,-1)∪(1,+∞),
又∵h(-x)=log3
-2x,
∴h(x)+h(-x)=log3
+log3
+2x-2x=0,
故h(x)为奇函数;
(Ⅱ)∵f(x)=log3g(x),
∴
=-2ax+a+1,且x∈(-∞,-1)∪(1,+∞),
∴(1-2x)a=
-1=-
,
显然a≠0,
∴
=(x+1)(x-
),
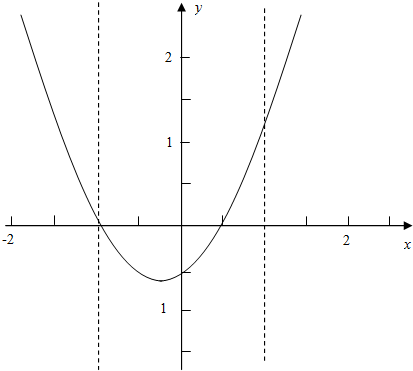
利用图象可知,当
>1时,
方程
=(x+1)(x-
)在(-∞,-1)∪(1,+∞)内有两个不等实数根,
解得0<a<1.
 (Ⅰ)证明:当a=-1时,
(Ⅰ)证明:当a=-1时,f(x)=log3
| x-1 |
| x+1 |
h(x)=log3
| x-1 |
| x+1 |
定义域为(-∞,-1)∪(1,+∞),
又∵h(-x)=log3
| x+1 |
| x-1 |
∴h(x)+h(-x)=log3
| x-1 |
| x+1 |
| x+1 |
| x-1 |
故h(x)为奇函数;
(Ⅱ)∵f(x)=log3g(x),
∴
| x-1 |
| x+1 |
∴(1-2x)a=
| x-1 |
| x+1 |
| 2 |
| x+1 |
显然a≠0,
∴
| 1 |
| a |
| 1 |
| 2 |
利用图象可知,当
| 1 |
| a |
方程
| 1 |
| a |
| 1 |
| 2 |
解得0<a<1.
看了已知函数f(x)=log3x-...的网友还看了以下:
关于X的一元二次方程2X^2-tx-2=0有两个实根α、β ,设f(x)关于x的一元二次方程2x^ 2020-05-16 …
已知X1,X2是关于X的方程X的平方-KX+(5K-5)=0的两个正实数根,且满足2X1+X2=7 2020-05-16 …
初三数学题!求解谢谢啦要有过程啦谢谢!1、已知关于x的方程(m-1)x²-(m-2)x-2m=0. 2020-05-22 …
在代数学中,为了表述的简洁,常用记号f(x),g(x),P(x),……已知关于x的实系数多项式P( 2020-06-12 …
已知:关于x的一元二次方程kx2-(k-1)x-1=0(1)求证:方程有两个实数根;(2)当k为何 2020-07-30 …
求两条关于集合的题目的解法1,若集合A=(y|y=x平方+2x+4,x属于实数),B=(y|y=a 2020-07-30 …
已知a,b,c是△ABC的∠A,∠B,∠C对边,a>b,关于x的方程x²-2(a+b)x+2ab+ 2020-07-30 …
有两个正实数根、无实数根是什么意思1)已知方程ax^2+2x+c=0有两个正实数根,则P(a,c)关 2020-12-08 …
求证:关于一元二次方程x^-mx+m^-4=0有两个正实根的充要条件是:2<m≤三分之四倍根号三.有 2021-01-13 …
已知关于x的方程x方+px+q=0有两个负实数根,则p,q满足的条件~已知关于y的方程y方-ay+a 2021-01-16 …