早教吧作业答案频道 -->数学-->
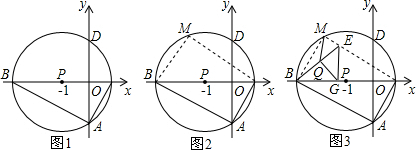
如图1,以点P(-1,0)为圆心的圆,交x轴于B,C两点(B在C的左侧),交y轴于A,D两点(A在D的下方).AD=23.(1)求B,C两点的坐标;(2)如图2,将△ABC绕点P旋转180°得到△MCB,请在图中画
题目详情
如图1,以点P(-1,0)为圆心的圆,交x轴于B,C两点(B在C的左侧),交y轴于A,D两点(A在D的下方).AD=2
.
(1)求B,C两点的坐标;
(2)如图2,将△ABC绕点P旋转180°得到△MCB,请在图中画出线段MB,MC,判断四边形ACMB的形状,并说明理由;
(3)如图3,动点E在CM上,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ,QG,求证:∠MQG的大小为定值.
| 3 |
(1)求B,C两点的坐标;
(2)如图2,将△ABC绕点P旋转180°得到△MCB,请在图中画出线段MB,MC,判断四边形ACMB的形状,并说明理由;
(3)如图3,动点E在CM上,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ,QG,求证:∠MQG的大小为定值.

▼优质解答
答案和解析
(1)连接PA,如图1所示.
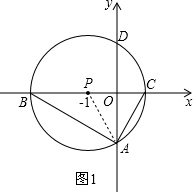
∵PO⊥AD,
∴AO=DO.
∵AD=2
,
∴OA=
.
∵点P坐标为(-1,0),
∴OP=1.
∴PA=
=
=2,
∴BP=CP=2,
∴OB=2+1=3,OC=2-1=1.
∴B(-3,0),C(1,0).
(2)连接AP,延长AP交 P于点M,连接MB、MC.
如图2所示,线段MB、MC即为所求作.
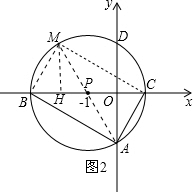
四边形ACMB是矩形.理由如下:
∵△MCB由△ABC绕点P旋转180°所得,
∴四边形ACMB是平行四边形.
∵BC是 P的直径,
∴∠CAB=90°.
∴平行四边形ACMB是矩形.
过点M作MH⊥BC,垂足为H,如图2所示.
在△MHP和△AOP中,
∵
,
∴△MHP≌△AOP(AAS).
∴MH=OA=
,PH=PO=1.
∴OH=2.
∴点M的坐标为(-2,
).
(3)在旋转过程中∠MQG的大小不变.
∵四边形ACMB是矩形,
∴∠BMC=90°.
∵EG⊥BO,
∴∠BGE=90°.
∴∠BMC=∠BGE=90°.
∵点Q是BE的中点,
∴QM=QE=QB=QG.
∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图3所示.
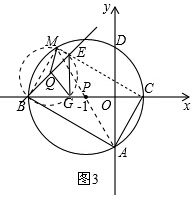
∴∠MQG=2∠MBG.
∵OA=
,OP=1,∠AOP=90°,
∴∠APC=60°,
∵PC=PA,
∴∠PCA=∠

∵PO⊥AD,
∴AO=DO.
∵AD=2
| 3 |
∴OA=
| 3 |
∵点P坐标为(-1,0),
∴OP=1.
∴PA=
| OP2+OA2 |
12+(
|
∴BP=CP=2,
∴OB=2+1=3,OC=2-1=1.
∴B(-3,0),C(1,0).
(2)连接AP,延长AP交 P于点M,连接MB、MC.
如图2所示,线段MB、MC即为所求作.

四边形ACMB是矩形.理由如下:
∵△MCB由△ABC绕点P旋转180°所得,
∴四边形ACMB是平行四边形.
∵BC是 P的直径,
∴∠CAB=90°.
∴平行四边形ACMB是矩形.
过点M作MH⊥BC,垂足为H,如图2所示.
在△MHP和△AOP中,
∵
|
∴△MHP≌△AOP(AAS).
∴MH=OA=
| 2 |
∴OH=2.
∴点M的坐标为(-2,
| 2 |
(3)在旋转过程中∠MQG的大小不变.
∵四边形ACMB是矩形,
∴∠BMC=90°.
∵EG⊥BO,
∴∠BGE=90°.
∴∠BMC=∠BGE=90°.
∵点Q是BE的中点,
∴QM=QE=QB=QG.
∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图3所示.

∴∠MQG=2∠MBG.
∵OA=
| 3 |
∴∠APC=60°,
∵PC=PA,
∴∠PCA=∠
看了如图1,以点P(-1,0)为圆...的网友还看了以下:
若函数f(x,y)在点(x0,y0)处沿任意方向的方向导数都存在,则()A.f(x,y)在点(x0 2020-05-14 …
概率与统计问题!求D(X+Y)和D(X-Y)的值设随机变量X的方差D(X)=16,随机变量Y的方差 2020-06-10 …
设D是一有界闭域,函数f(x,y)在D上连续,在D内偏导数存在,且满足等式∂f(x,y)∂x+2∂ 2020-06-23 …
如图所示,将某正粒子放射源置于原点O,其向各方向射出的粒子速度大小均为v0、质量均为m、电荷量均为 2020-07-07 …
设D是一有界闭域,函数f(x,y)在D上连续,在D内偏导数存在,且满足等式?f(x,y)?x+2? 2020-07-31 …
偏微分方程差分成矩阵二维,二阶,想差分成矩阵Au=b的形式求数值解,现在x.y方向各有34个点,想 2020-08-02 …
分式(要求有过程)1、计算(x-y+4xy/x+y)(x+y-4xy/x+y)的结果()A.y方-a 2020-10-31 …
请问:求三元函数f(x,y,z)=x+y+z在曲面S:x平方+y平方=z和平面z=1围成的闭区域D上 2020-11-01 …
如图所示,真空中有一以O点为圆心的圆形匀强磁场区域,半径为R,磁场垂直纸面向里,在y>R的区域存在沿 2020-11-01 …
(2013•宜宾)根据经纬网图,回答问题.(1)写出D地的经纬度.经度:,纬度:.(2)B在D的方向 2020-11-12 …