阅读下面材料：小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA=3，PB=4，PC=5，求∠APB的度数．小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到

Question

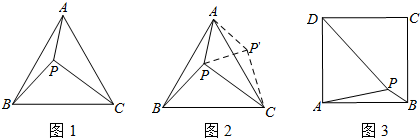
阅读下面材料：
小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA=3，PB=4，PC=5，求∠APB的度数．  小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决．
（1）请你回答：图1中∠APB的度数等于___．
参考小伟同学思考问题的方法，解决下列问题：
（2）如图3，在正方形ABCD内有一点P，且PA=2 √(2)，PB=1，PD= √(17)，求∠APB的度数和正方形的边长．

Answer 1

（1）如图2，把△APB绕点A逆时针旋转60°得到△ACP′，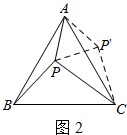
由旋转的性质，P′A=PA=3，P′D=PB=4，∠PAP′=60°，
∴△APP′是等边三角形，
∴PP′=PA=3，∠AP′P=60°，
∵PP′²+P′C²=3²+4²=25，PC²=5²=25，
∴PP′²+P′C²=PC²，
∴∠PP′C=90°，
∴∠AP′C=∠AP′P+∠PP′C=60°+90°=150°；
故∠APB=∠AP′C=150°；
故答案为150°．
（2）如图3，把△APB绕点A逆时针旋转90°得到△ADP′，
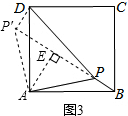由旋转的性质，P′A=PA=2√(2)，P′D=PB=1，∠PAP′=90°，
∴△APP′是等腰直角三角形，
∴PP′=√(2)PA=√(2)×2√(2)=4，∠AP′P=45°，
∵PP′²+P′D²=4²+1²=17，PD²=（√(17)^）2=17，
∴PP′²+P′D²=PD²，
∴∠PP′D=90°，
∴∠AP′D=∠AP′P+∠PP′D=45°+90°=135°，
故∠APB=∠AP′D=135°，
∵∠APB+∠APP′=135°+45°=180°，
∴点P′、P、B三点共线，
过点A作AE⊥PP′于E，
则AE=PE=(1)/(2)PP′=(1)/(2)×4=2，
∴BE=PE+PB=2+1=3，
在Rt△ABE中，AB=√(AE2+BE2)=√(22+32)=√(13)．