(本题满分12分)如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D.(1)如图1,连接BD并延长BD交AC于点E,连接AD.①证明:△CDE∽△CAD;②若AB=2
(本题满分12分)
如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D.
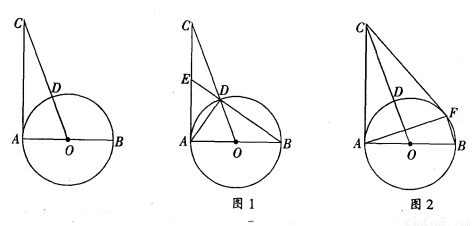
(1)如图1,连接BD并延长BD交AC于点E,连接AD.
①证明:△CDE∽△CAD;
②若AB=2,AC=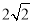 .求CD和CE的长;
.求CD和CE的长;
(2)如图2,过点C作⊙O的另一条切线,切点为F,连结AF、BF,若OC=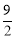 BF,求
BF,求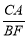 的值.
的值.
分 析:
(1)由AC是⊙O的切线,得到∠1+∠BAD=90°,又由AB是⊙O的直径,得到∠B+∠BAD=90°,故有∠1=∠B,又由OB=OD,得到∠2=∠B,又因∠2=∠3,得到∠3=∠B,得到∠1=∠3,由∠C=∠C,得到△CDE∽△CAD;(2)在Rt△AOC中,算出OC,进而算出CD的长,由△CDE∽△CAD,得到,解出CE的长;(3)由△ABF∽△COA,得到,故,又OC=BF,AB=2r,OA=r,得到,得到BF=,OC=3r,在Rt△COA中,由勾股定理求出CA的长,再算.试题
解析:
(1)证明:∵AC是⊙O的切线,∴∠1+∠BAD=90°,又∵AB是⊙O的直径,∴∠B+∠BAD=90°,∴∠1=∠B,又∵OB=OD,∴∠2=∠B,又∵∠2=∠3,∴∠3=∠B,∴∠1=∠3,∵∠C=∠C,∴△CDE∽△CAD;(2)在Rt△AOC中,OC=,∴CD=OC-OD=3-1=2,∵△CDE∽△CAD,∴,即,∴CE=;(3)由△ABF∽△COA,∴,∴,又OC=BF,AB=2r,OA=r(r为⊙O的半径),∴,∴BF=,OC=3r,在Rt△COA中,由勾股定理知:CA=,∴.
考点:
圆的综合题.
股份有限公司董事会须有( )的董事出席方可举行。A.1/3 以上B.1/2 C.1/2以上D.2/3 2020-05-27 …
一年以内有醉酒后驾驶营运机动车的行为,被处罚()的,吊销驾驶证。A.3次以上B.1次C.2次以上D. 2020-05-31 …
根据《期货交易所管理办法》的规定,理事会召开至少要有( )理事出席。 A.2/3以上B.1/3以上C 2020-06-04 …
手术前呼吸道准备戒烟时间应选择 ()A.3日以上B.1周以上C.3周以上D.2周以上 2020-06-07 …
手术前呼吸道准备戒烟时间应选择: ()A.3日以上B.1 周以上C.2周以上D.3周以上 2020-06-07 …
1已知点A(a,2)和点B(-1,b)根据下列条件求出a,b的值.(1)A、B在坐标轴上、(2)A 2020-06-14 …
判断题(判断下列各题是否正确,正确的请在括号内填上“A”,错误的请在括号内填上“B”)1.消费者的合 2020-12-21 …
若绝对值ab-2加上(b-1)=0求ab分之1+(a+1)(b+1)分之1+(a+2)(b+2)分之 2020-12-31 …
对于任意有理数a、b定义运算*如下:a*b=ab+a-b(1).求1*(-2)(-2)*1的值;(2 2021-01-20 …
判断题(判断下列各题是否正确,正确的请在括号内填上“A”,错误的请在括号内填上“B”)1.生活理想是 2021-01-30 …