早教吧作业答案频道 -->数学-->
已知:正方形ABCD的边长为4,点E为BC边的中点,点P为AB边上一动点,联结PE,过E作EQ⊥PE交边CD于Q,直线PQ交直线AD于点G.(1)如图,当BP=1.5时,求CQ的长;(2)如图,当点G在射线AD上时,设B
题目详情
已知:正方形ABCD的边长为4,点E为BC边的中点,点P为AB边上一动点,联结PE,过E作EQ⊥PE交边CD于Q,直线PQ交直线AD于点G.
(1)如图,当BP=1.5时,求CQ的长;
(2)如图,当点G在射线AD上时,设BP=x,DG=y,求y关于x的函数关系式,并写出x的取值范围.
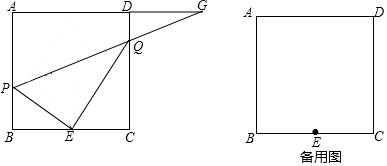
(1)如图,当BP=1.5时,求CQ的长;
(2)如图,当点G在射线AD上时,设BP=x,DG=y,求y关于x的函数关系式,并写出x的取值范围.

▼优质解答
答案和解析
(1)∵点E为BC边的中点,
∴BE=CE=2,
∵EQ⊥PE,
∴∠PEQ=90°,
∴∠PEB+∠QEC=∠EQC+∠QEC=90°,
∴∠PEB=∠EQC,
∵∠B=∠C=90°,
∴△PEB∽△EQC,
∴
=
∴CQ=
,
(2)由(1)可知:△PEB∽△EQC,
∴
=
∴CQ=
,
当CQ=4时,
此时x=1,
∴1≤x≤4,
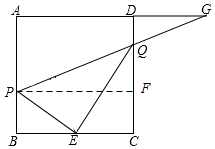
过点P作PF⊥CD于点F,
∴△QPF∽△QGD,
∴
=
∵CF=PB=x,
∴QF=CQ-CF=
-x,
DQ=CD-CQ=4-
∴
=
,
化简可得:y=
(1≤x≤4)
∴BE=CE=2,
∵EQ⊥PE,
∴∠PEQ=90°,
∴∠PEB+∠QEC=∠EQC+∠QEC=90°,
∴∠PEB=∠EQC,
∵∠B=∠C=90°,
∴△PEB∽△EQC,
∴
| PB |
| EC |
| BE |
| CQ |
∴CQ=
| 8 |
| 3 |
(2)由(1)可知:△PEB∽△EQC,
∴
| PB |
| EC |
| BE |
| CQ |

∴CQ=
| 4 |
| x |
当CQ=4时,
此时x=1,
∴1≤x≤4,
过点P作PF⊥CD于点F,
∴△QPF∽△QGD,
∴
| PF |
| DG |
| QF |
| DQ |
∵CF=PB=x,
∴QF=CQ-CF=
| 4 |
| x |
DQ=CD-CQ=4-
| 4 |
| x |
∴
| 4 |
| y |
| ||
4-
|
化简可得:y=
| 4(4x-4) |
| 4-x2 |
看了 已知:正方形ABCD的边长为...的网友还看了以下:
如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△ 2020-04-07 …
如图,正方形ABCD的边长为1,G是CD边上的一个动点(G不与C、D重合),以CG为一边向正方如图 2020-05-16 …
接到后面出现超越方程,谢谢伸出援手g(x)=2lnx-ax^2+x-e/a+1/2,当a>0时讨论 2020-06-27 …
如图:已知AB=10,点C、D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP、PB 2020-07-09 …
如图.在矩形ABCD中.AB=12cm.BC=8cm.点E.F.G分别从A.B.C三点同时出发延矩 2020-07-16 …
如图:已知AB=10,点C、D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP、PB为 2020-11-26 …
如图甲所示,若绷紧水平的传送皮带以稳定的速率运行,今在A点轻轻放上一个小行李,小行李从A点运动至B点 2020-12-14 …
如图,已知AB=5,点C、D在线段AB上且AC=DB=1,P是线段CD上的动点,分别以AP、PB为边 2020-12-27 …
如图,在矩形ABCD中,点P在AD上,AB=2,AP=1,E是AB上的一个动点,连接PE,过点P作P 2020-12-27 …
如图,在正方形ABCD中,G是BC上的任意一点(G与B,C两点不重合),E,F是AG上的两点(E,F 2021-01-11 …