早教吧作业答案频道 -->数学-->
已知数列an的相邻两项an,an+1满足,且a1=1(1)求证是等比数列(2)求数列{an}的通项公式an及前n项和Sn.
题目详情
已知数列a n 的相邻两项a n ,a n+1 满足 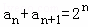 ,且a 1 =1
,且a 1 =1
(1)求证 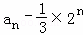 是等比数列
是等比数列
(2)求数列{a n }的通项公式a n 及前n项和S n .
▼优质解答
答案和解析
考点:
数列递推式;等比关系的确定;数列的求和.
专题:
计算题;等差数列与等比数列.
分析:
(1)由,得=﹣(),由此能证明数列{}是等比数列. (2)由,知Sn={(2+22+23+…+2n)﹣[﹣(﹣1)+(﹣1)2+…+(﹣1)n]},由此能求出数列{an}的通项公式an及前n项和Sn.
(1)由, 得=﹣(), 故数列{}是首项为=,公比为﹣1的等比数列. (2)由(1)知, 即, Sn=a1+a2+a3+…+an ={(2+22+23+…+2n)﹣[﹣(﹣1)+(﹣1)2+…+(﹣1)n]} =(2n+1﹣2﹣) =﹣(﹣1)n﹣.
点评:
本题考查等比数列的证明,考查数列的通项公式和数列的前n项和的求法,解题时要认真审题,注意等价转化思想的合理运用.
考点:
数列递推式;等比关系的确定;数列的求和.
专题:
计算题;等差数列与等比数列.
分析:
(1)由,得=﹣(),由此能证明数列{}是等比数列. (2)由,知Sn={(2+22+23+…+2n)﹣[﹣(﹣1)+(﹣1)2+…+(﹣1)n]},由此能求出数列{an}的通项公式an及前n项和Sn.
(1)由, 得=﹣(), 故数列{}是首项为=,公比为﹣1的等比数列. (2)由(1)知, 即, Sn=a1+a2+a3+…+an ={(2+22+23+…+2n)﹣[﹣(﹣1)+(﹣1)2+…+(﹣1)n]} =(2n+1﹣2﹣) =﹣(﹣1)n﹣.
点评:
本题考查等比数列的证明,考查数列的通项公式和数列的前n项和的求法,解题时要认真审题,注意等价转化思想的合理运用.
看了 已知数列an的相邻两项an,...的网友还看了以下:
1.已知数列{An}满足{An/n}是公差为1,的等差数列,且An+1=(n+2/n)·An+1( 2020-04-09 …
8.在等差数列{an}中,若a1=2,a2+a3=13,则a4+a5+a6=多少?9.已知等差数列 2020-05-14 …
30min内解决分数双倍设sn是等比数列{an}前n项,且s3,s9,s6成等差数列(1)若a2, 2020-06-03 …
已知等差数列{an},Sn为其前n项和,a5=9,S5=25;数列{bn}满足bn=1an•an+ 2020-06-27 …
再来两个等比数列题(高中数学)page1291)已知等比数列{an}前3项的和是9/2,前6项的和 2020-07-18 …
函数数列已知点(1,1/3)是函数f(x)=a^x(a>0,且a不等于1)的图像上的一点,等比数列 2020-07-21 …
已知数列是等比数列a2等于4an的前2项和等于6前2项和等于6.求通项公式.设a1b1+a2b2+ 2020-07-27 …
已知等比数列的前n项和Sn=4的n次方+a则a的值等于()A.-4B.-1C.0D.1∵等比数列{ 2020-07-27 …
等比数列的倒数求和等比数列(an)的首项a1=1,公比为q,前n项和是Sn,则数列(1/an)的前 2020-07-28 …
关于数列的已知等比数列{an}的前n项和An=(1/3)^n-c(c为常数),数列{bn}(bn> 2020-07-30 …