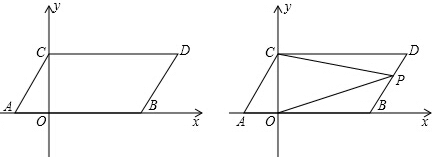
如图1，在平面直角坐标系中，点A，B的坐标分别为A（m，0），B（n，0）且m、n满足|m+2|+5-n=0，现同时将点A，B分别向上平移3个单位，再向右平移2个单位，分别得到点A，B的对应点C，D，连接AC

Question

如图1，在平面直角坐标系中，点A，B的坐标分别为A（m，0），B（n，0）且m、n满足|m+2|+√(5-n)=0，现同时将点A，B分别向上平移3个单位，再向右平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
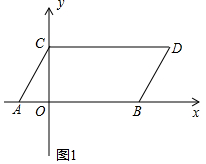
（1）求点C，D的坐标及四边形OBDC的面积；
（2）如图2，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合），试探究∠DCP，∠BOP与∠CPO的数量关系，并说明理由；
（3）在四边形OBDC内是否存在一点P，连接PO，PB，PC，PD，使S_△PCD=S_△PBD；S_△POB：S_△POC=5：6，若存在这样一点，求出点P的坐标，若不存在，试说明理由．

Answer 1

（1）|m+2|+√(5-n)=0，
∴m=-2，n=5，
∴A（-2，0），B（5，0），
∵点A，B分别向上平移3个单位，再向右平移2个单位，
∴C（0，3），D（7，2）；
∵OB=5，
∴S_{四边形OBDC}=(1)/(2)（5+7）×3=18；

（2）∠DCP+∠BOP=∠CPO．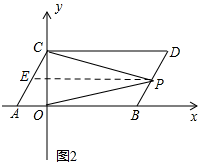
理由：由平移的性质可得AB∥CD，
如图2，过点P作PE∥AB，则PE∥CD，
∴∠DCP=∠CPE，∠BOP=∠OPE，
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP，
∴∠DCP，∠BOP与∠CPO的数量关系为：∠DCP+∠BOP=∠CPO；

（3）存在，
如图3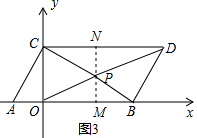，过P作PM⊥OB于M，交CD于N，
∵CD∥OB，
∴PN⊥CD，
设P（m，n），
∵S_△POB：S_△POC=5：6，
∴(1)/(2)×5•n=(1)/(2)×3•m，
∴m=(5)/(3)n，①
∵S_△PCD=S_△PBD，
∴(1)/(2)×7•（3-n）=(1)/(2)（5-m+7-m）×3-(1)/(2)（5-m）n-(1)/(2)（7-m）（3-n），②
由①、②解得m=4，n=2，
∴P（4，2）．
故存在这样一点P，使S_△PCD=S_△PBD；S_△POB：S_△POC=5：6．