早教吧作业答案频道 -->数学-->
在平面直角坐标系中,直线y=-512x+5与x轴、y轴分别交于点A、B,P是射线AB上一动点,设AP=a,以AP为直径作C.(1)求cos∠ABO的值;(2)当a为何值时,C与坐标轴恰有3个公共点;(3)过P作PM⊥
题目详情
在平面直角坐标系中,直线y=-
x+5与x轴、y轴分别交于点A、B,P是射线AB上一动点,设AP=a,以AP为直径作 C.
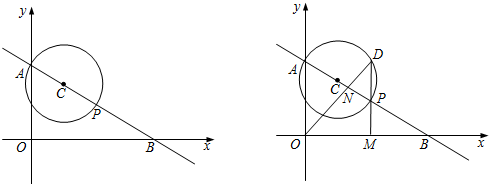
(1)求cos∠ABO的值;
(2)当a为何值时, C与坐标轴恰有3个公共点;
(3)过P作PM⊥x轴于M,与 C交于点D,连接OD交AB于点N,若∠ABO=∠D,求a的值.
| 5 |
| 12 |
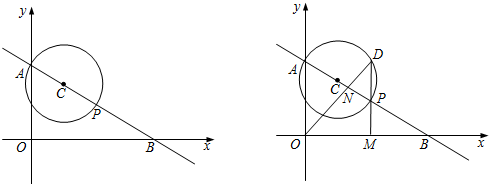
(1)求cos∠ABO的值;
(2)当a为何值时, C与坐标轴恰有3个公共点;
(3)过P作PM⊥x轴于M,与 C交于点D,连接OD交AB于点N,若∠ABO=∠D,求a的值.
▼优质解答
答案和解析
(1)∵直线y=-
x+5与x轴、y轴分别交于点A、B,
∴A (0,5),B (12,0),
∴AO=5,BO=12.
∵AO⊥BO,
∴AB=
=13,
∴cos∠ABO=
=
;
(2) C与坐标轴恰有3个公共点时, C过原点O或 C与OB相切,
① C过原点O,
∴a=AB=13;
②如图1, C与OB相切,设切点为H,连接CH,则CH⊥OB,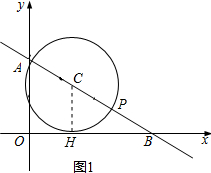
∵AO⊥OB,
∴△BCH∽△BAO,
∴
=
,
∴
=
,
∴a=
.
综上所述:a=13或a=
;
(3)如图2,连接AD,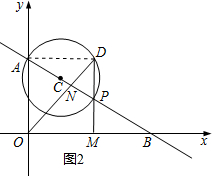
∵AP是直径,
∴∠ADP=90°,
∵PM⊥x轴,
∴∠DMB=90°.
∵∠ABO=∠ODM,∠NPD=∠BPM,
∴∠DNP=∠BMP=90°,
∴∠ABO=90°-∠DOM=∠AOD,
∴tan∠AOD=tan∠ABO=
=
,
PM⊥x轴,AO⊥x轴,∠ADP=90°,
∴∠OAD=90°,
在Rt△ADO中,tan∠AOD=
=
,
∴AD=
×5=
,
又∵∠DAP=∠ABO,
在Rt△ADO中,cos∠DAP=
,
∴AP=
=
=
×
=
,
∴a=AP=
.
| 5 |
| 12 |
∴A (0,5),B (12,0),
∴AO=5,BO=12.
∵AO⊥BO,
∴AB=
| OA2+OB2 |
∴cos∠ABO=
| BO |
| AB |
| 12 |
| 13 |
(2) C与坐标轴恰有3个公共点时, C过原点O或 C与OB相切,
① C过原点O,
∴a=AB=13;
②如图1, C与OB相切,设切点为H,连接CH,则CH⊥OB,

∵AO⊥OB,
∴△BCH∽△BAO,
∴
| BC |
| BA |
| CH |
| AO |
∴
13-
| ||
| 13 |
| ||
| 5 |
∴a=
| 65 |
| 9 |
综上所述:a=13或a=
| 65 |
| 9 |
(3)如图2,连接AD,

∵AP是直径,
∴∠ADP=90°,
∵PM⊥x轴,
∴∠DMB=90°.
∵∠ABO=∠ODM,∠NPD=∠BPM,
∴∠DNP=∠BMP=90°,
∴∠ABO=90°-∠DOM=∠AOD,
∴tan∠AOD=tan∠ABO=
| AO |
| BO |
| 5 |
| 12 |
PM⊥x轴,AO⊥x轴,∠ADP=90°,
∴∠OAD=90°,
在Rt△ADO中,tan∠AOD=
| AD |
| AO |
| 5 |
| 12 |
∴AD=
| 5 |
| 12 |
| 25 |
| 12 |
又∵∠DAP=∠ABO,
在Rt△ADO中,cos∠DAP=
| AD |
| AP |
∴AP=
| AD |
| cos∠DAP |
| AD |
| cos∠ABO |
| 25 |
| 12 |
| 13 |
| 12 |
| 325 |
| 144 |
∴a=AP=
| 325 |
| 144 |
看了 在平面直角坐标系中,直线y=...的网友还看了以下:
和直线l都相交的两条直线不能确定一个平面?为什么?虽然有多种情况可是也可以确定1个平面啊?难道这个 2020-05-14 …
如图,平面直角坐标系中,点A的坐标为(-1,0)点P从原点O,沿x轴正方向以每秒1个单位长度运动运 2020-05-15 …
已知直线l1:y=-12x+2与直线l2:y=2x-3相交于点A.(1)求点A坐标;(2)设l1交 2020-07-16 …
星期一之前)1.chat过去式2.两条直线相交有几个交点?3条直线相交最多有几个相交?4条直线相交 2020-07-17 …
在直角坐标系中,直线L经过点(2,3)和(-1,-3)直线L2经过原点,且与直线L1交于(-2,a 2020-07-21 …
二元一次方程与一次函数,在平面直角坐标系中,直线L1经过点(2,3)和(-1,-3),直线L2经过 2020-08-03 …
二元一次方程与一次函数,设一次函数Y=3X-4与Y=-X+3的图像的交点为P,它们与X轴分别交于点 2020-08-03 …
如图1,点A为抛物线C1:y=x2﹣2的顶点,点B的坐标为(1,0)直线AB交抛物线C1于另一点C( 2020-10-31 …
在平面直角坐标系中,直线y=kx+b经过点(2,3)和点(-1,-3),直线y=mx与直线y=kx+ 2020-11-03 …
已知:一次函数y=2x与y=-x+3的图像如图所示,直线l平行于y轴,交直线y=2x与于点p,交直线 2020-11-27 …