早教吧作业答案频道 -->数学-->
如图,在等边三角形ABC中,点M是BC边上的任意一点(不与端点重合),连接AM,以AM为边作等边三角形AMN,连接CN.(1)求∠ACN的度数.(2)若点M在△ABC的边BC的延长线上,其他条件不变,
题目详情
如图,在等边三角形ABC中,点M是BC边上的任意一点(不与端点重合),连接AM,以AM为边作等边三角形AMN,连接CN.
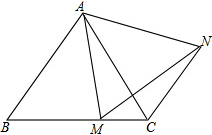
(1)求∠ACN的度数.
(2)若点M在△ABC的边BC的延长线上,其他条件不变,则∠ACN的度数是否发生变化?(直接写出结论即可)

(1)求∠ACN的度数.
(2)若点M在△ABC的边BC的延长线上,其他条件不变,则∠ACN的度数是否发生变化?(直接写出结论即可)
▼优质解答
答案和解析
(1)证明:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∠B=60°,
∴∠BAM=∠CAN,
在△BAM和△CAN中,
,
∴△BAM≌△CAN(SAS),
∴∠ACN=∠B=60°;
(2) 结论∠ACN=60°仍成立.如图,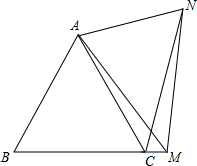
理由如下:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
在△BAM和△CAN中,
,
∴△BAM≌△CAN(SAS),
∴∠ACN=∠B=60°.
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∠B=60°,
∴∠BAM=∠CAN,
在△BAM和△CAN中,
|
∴△BAM≌△CAN(SAS),
∴∠ACN=∠B=60°;
(2) 结论∠ACN=60°仍成立.如图,

理由如下:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
在△BAM和△CAN中,
|
∴△BAM≌△CAN(SAS),
∴∠ACN=∠B=60°.
看了 如图,在等边三角形ABC中,...的网友还看了以下:
有甲,已两筐水果,甲筐水果重为(m-1)的平方kg,已筐水果重为(m的平方-1)kg(其中m大于1 2020-04-26 …
有甲乙两筐水果,甲筐水果重为(m-1)²kg,乙筐水果重为(m²-1)kg,(其中m>1),售完后 2020-04-26 …
1.在一根弹簧下端悬挂重为15N的重物,静止时弹簧长20cm,当这根弹簧下端悬挂重21N的重物静止 2020-05-14 …
如图所示,a、b为两根相连的轻质弹簧,它们的劲度系数分别为100N/m和200N/m,原长分别为6 2020-05-14 …
一只长方形纸片有一条边与正方形纸片边长相等,且其面积分别为:m^2-4n^2和m^2-4mn+4n 2020-07-03 …
关于弹簧的问题,劲力系数分别为10N/M与20N/M的弹簧,把20N/M的弹簧挂在另一个弹簧上,不 2020-07-16 …
某型铁路货车自重24t载重64t该车辆的每沿米轨道重为8t/m求车辆的自重系数2轴重3车辆的全长 2020-11-20 …
如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝 2020-12-02 …
定积分在物理学上的应用.一球形储液罐,半径为10cm,盛有比重为8KN/m的某种液体,液面距离罐定积 2020-12-05 …
如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无 2020-12-17 …