早教吧作业答案频道 -->数学-->
已知数列{an}的前n项和,数列{bn}满足.(1)求数列{an}的通项公式,并说明{an}是否为等比数列;(2)求数列的前n项和前Tn;(3)若-对任意的n∈N*恒成立,求t的最小正整
题目详情
已知数列{a n }的前n项和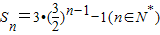 ,数列{b n }满足
,数列{b n }满足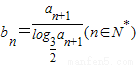 .
.
(1)求数列{a n }的通项公式,并说明{a n }是否为等比数列;
(2)求数列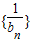 的前n项和前T n ;
的前n项和前T n ;
(3)若-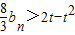 对任意的n∈N * 恒成立,求t的最小正整数值.
对任意的n∈N * 恒成立,求t的最小正整数值.
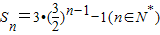 ,数列{b n }满足
,数列{b n }满足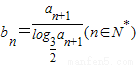 .
.(1)求数列{a n }的通项公式,并说明{a n }是否为等比数列;
(2)求数列
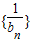 的前n项和前T n ;
的前n项和前T n ;(3)若-
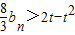 对任意的n∈N * 恒成立,求t的最小正整数值.
对任意的n∈N * 恒成立,求t的最小正整数值.▼优质解答
答案和解析
分析:
(1)利用数列递推式,再写一式,两式相减可得数列通项,利用等比数列的定义可得结论;(2)确定数列的通项,利用错位相减法求数列的和;(3)确定bn的最小值为b2=b3=,从而将不等式转化为t的不等式,即可求得结论.
(1)当n=1时,a1=S1=3×1-1=2;当n≥2时,an=Sn-Sn-1=∴∵n=1时,a1=S1=3×1-1=2不满足∴{an}不是等比数列;(2)∵=,∴=∴数列的前n项和前Tn=∴两式相减可得=∴Tn=(3)由(2)有bn+1-bn==∴n≤2时,有bn+1-bn≤0;n>2时,bn+1-bn>0∴bn的最小值为b2=b3=∴-等价于-∴t2-2t-3>0∴t>3或t<-1∴t的最小正整数值是4.
点评:
本题考查数列的通项与求和,考查恒成立问题,考查错位相减法的运用,考查学生分析解决问题的能力,属于中档题.
分析:
(1)利用数列递推式,再写一式,两式相减可得数列通项,利用等比数列的定义可得结论;(2)确定数列的通项,利用错位相减法求数列的和;(3)确定bn的最小值为b2=b3=,从而将不等式转化为t的不等式,即可求得结论.
(1)当n=1时,a1=S1=3×1-1=2;当n≥2时,an=Sn-Sn-1=∴∵n=1时,a1=S1=3×1-1=2不满足∴{an}不是等比数列;(2)∵=,∴=∴数列的前n项和前Tn=∴两式相减可得=∴Tn=(3)由(2)有bn+1-bn==∴n≤2时,有bn+1-bn≤0;n>2时,bn+1-bn>0∴bn的最小值为b2=b3=∴-等价于-∴t2-2t-3>0∴t>3或t<-1∴t的最小正整数值是4.
点评:
本题考查数列的通项与求和,考查恒成立问题,考查错位相减法的运用,考查学生分析解决问题的能力,属于中档题.
看了 已知数列{an}的前n项和,...的网友还看了以下:
已知数列{an},其前n项和Sn满足Sn+1=2XSn+1(X是>0的常数),且a1=1,a3=4 2020-05-13 …
数列{an}的前项n的和为Sn,存在常数A、B、C,使得an+Sn=An^2+Bn+C对任意正整数 2020-05-16 …
高二‘推理与证明’章节题目.“因为无理数是无限小数,而1/3是无限小数,所以1/3是无理数.”在以 2020-05-22 …
数学里的单位其实也是与实际计算有联系的,比如速度单位:千米/小时,它的写法就是来源于用总千米数除以 2020-05-22 …
已知数列{an}中,a1=1,对任意正整数n,均有a(n+1)=2an(1)求a3的值(2)求数列 2020-05-23 …
已知等差数列{an}满足a1+a(2n-1)=2n设Sn是数列{1/an}的前n项和,记f(n)= 2020-06-03 …
设数列的前项和为,对任意的正整数,都有成立,记。(1)求数列与数列的通项公式;(2)记,设数列的前 2020-06-11 …
a是无理数.证明:对任意正整数m,集合{n*a,n是整数}中必定存在某元素,它的小数点后的前m为小 2020-07-30 …
由键盘任意输入10个数,将最大数调到最前面,最小数调到最后面.输入:任意10个数输出:数据调整后的 2020-07-31 …
“指数函数y=ax(a>0且a≠1)是R上的增函数,而y=(12)x是指数函数,所以y=(12)x 2020-08-01 …