如图所示，已知平行六面体ABCD—A1B1C1D1的底面是菱形，且∠C1CB=∠C1CD=∠BCD=60°.(1)求证：CC1⊥BD;(2)当的值为多少时，能使A1C⊥平面C1BD？并

Question

如图所示，已知平行六面体 ABCD — A ₁ B ₁ C ₁ D ₁ 的底面是菱形，且∠ C ₁ CB =∠ C ₁ CD =∠ BCD =60°.

(1)求证： CC ₁ ⊥ BD ;

(2)当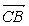 的值为多少时，能使 A ₁ C ⊥平面 C ₁ BD ？并加以证明.

Answer 1

思路
解析：
在平行六面体中，通常以同一顶点上三条棱所在的直线的方向向量为基向量，建立空间向量基底.(1)证明：取=a =b =c为空间的一个基底，设菱形的边长为a.∵=a-b，∴·=c·a-c·b＝|c||a|cos〈c a〉-|c||b|cos〈c b〉=|c|acos60°-|c|acos60°=0.∴⊥.∴⊥.(2)设=λ(λ＞0)，即||=λ||时，能使A1C⊥平面C1BD.∵C1D平面BC1D BD平面BC1D ∴A1C⊥C1D且A1C⊥BD.∴·=0且·=0.∵=-(a+b+c) =a-c，〈a b〉=〈b c〉=60° |a|=|b|=a，∴·=-(a+b+c)·(a-c)=-a2-aacos60°+a·cos60°+∴3λ2-λ-2=0.∵λ＞0 ∴λ=1.当λ=1时，·＝-(a+b+c)·(a-b)=-a2+a2-aacos60°+aacos60°=0，∴⊥.∴A1C⊥BD.同理，当λ=1时，⊥ 即A1C⊥BC1.由上述证明过程知当时，能使A1C⊥平面C1BD.方法归纳  向量法解决线面垂直问题时，通常转化为此直线的方向向量垂直于平面内两不共线的向量问题.