早教吧作业答案频道 -->数学-->
如图1、2、3、…、n,M、N分别是O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.(1)求图1中∠MON的度数;(2)图2中∠MON的度数是
题目详情
如图1、2、3、…、n,M、N分别是 O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.
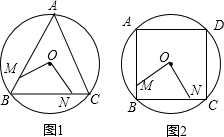
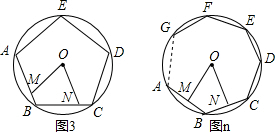
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是___,图3中∠MON的度数是___;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).


(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是___,图3中∠MON的度数是___;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
▼优质解答
答案和解析
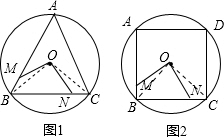 分别连接OB、OC,
分别连接OB、OC,
(1)∵AB=AC,
∴∠ABC=∠ACB,
∵OC=OB,O是外接圆的圆心,
∴CO平分∠ACB
∴∠OBC=∠OCB=30°,
∴∠OBM=∠OCN=30°,
∵BM=CN,OC=OB,
∴△OMB≌△ONC,
∴∠BOM=∠NOC,
∵∠BAC=60°,
∴∠BOC=120°;
∴∠MON=∠BOC=120°;
(2)同(1)可得∠MON的度数是90°,图3中∠MON的度数是72°;
(3)由(1)可知,∠MON=
=120°;在(2)中,∠MON=
=90°;在(3)中∠MON=
=72°…,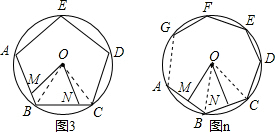
故当n时,∠MON=
.
 分别连接OB、OC,
分别连接OB、OC,(1)∵AB=AC,
∴∠ABC=∠ACB,
∵OC=OB,O是外接圆的圆心,
∴CO平分∠ACB
∴∠OBC=∠OCB=30°,
∴∠OBM=∠OCN=30°,
∵BM=CN,OC=OB,
∴△OMB≌△ONC,
∴∠BOM=∠NOC,
∵∠BAC=60°,
∴∠BOC=120°;
∴∠MON=∠BOC=120°;
(2)同(1)可得∠MON的度数是90°,图3中∠MON的度数是72°;
(3)由(1)可知,∠MON=
| 360° |
| 3 |
| 360° |
| 4 |
| 360° |
| 5 |

故当n时,∠MON=
| 360° |
| n |
看了 如图1、2、3、…、n,M、...的网友还看了以下:
已知数列{an}:a1,a2,…,an(n≥3),令集合T={x|x=ai+aj,1≤i<j≤n} 2020-05-14 …
关于正负数,绝对值a,c为小于0的数,即负数b大于0,即正数c小于aa+b的绝对值+b-c的绝对值 2020-05-24 …
excelA列不含B列两个数的删除ABC12323789123A含有B的两个数C保留237237A 2020-06-14 …
【数论:奇数与偶数】设a,b,c为整数,证明:(a+b+c)(a+b-c)(b+c-a)(c+a- 2020-06-27 …
数学问题:净增数比率计算公式现有一个用户净增数的公式需要计算:A(净增比率)=B(实际净增数)/C 2020-06-30 …
一道求数的题有一个2000位的数A能被9整除,数A的各个数位上的数字之和是B,数B的各个数位的数字 2020-07-31 …
2014年安徽理科数学21题的解答方法是什么啊?还是很难的,难怪是高考压轴题啊,毫无思路设实数c> 2020-08-01 …
已知函数f(x)=xex+x2+ax+b,在点(0,f(0))处的切线方程是x+y-1=0,其中e 2020-08-02 …
1.已知a是I-2I的相反数,b是3的相反数,c是负三分之一的绝对值的倒数的相反数,d是负二又三分之 2020-11-01 …
初一数学题1.设a是最小的自然数,b是最大的负整数,c是绝对值最少的有理数,则a-b+c的值为?2. 2020-11-17 …