早教吧作业答案频道 -->数学-->
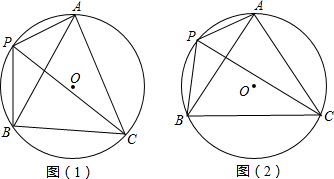
如图,已知△ABC是O的内接三角形,AB=AC,点P是AB的中点,连接PA,PB,PC.(1)如图①,若∠BPC=60°.求证:AC=3AP;(2)如图②,若sin∠BPC=2425,求tan∠PAB的值.
题目详情
如图,已知△ABC是 O的内接三角形,AB=AC,点P是
的中点,连接PA,PB,PC.
(1)如图①,若∠BPC=60°.求证:AC=
AP;
(2)如图②,若sin∠BPC=
,求tan∠PAB的值.
 |
| AB |
(1)如图①,若∠BPC=60°.求证:AC=
| 3 |
(2)如图②,若sin∠BPC=
| 24 |
| 25 |

▼优质解答
答案和解析
(1)∵∠BPC=60°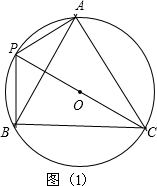
∴∠BAC=60°,
∵AB=AC,
∴△ABC为等边三角形,
∴∠ACB=∠ABC=60°,
∴∠APC=∠ABC=60°,
而点P是
的中点,
∴∠ACP=
∠ACB=30°,
∴∠PAC=90°,
∴tan∠PCA=
=tan30°=
,
∴AC=
PA;
(2)过A点作AD⊥BC交BC于D,连结OP交AB于E,如图,
∵AB=AC,
∴AD平分BC,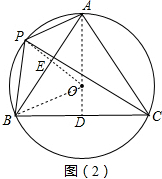
∴点O在AD上,
连结OB,则∠BOD=∠BAC,
∵∠BPC=∠BAC,
∴sin∠BOD=sin∠BPC=
=
,
设OB=25x,则BD=24x,
∴OD=
=7x,
在Rt△ABD中,AD=25x+7x=32x,BD=24x,
∴AB=
=40x,
∵点P是
的中点,
∴OP垂直平分AB,
∴AE=
AB=20x,∠AEP=∠AEO=90°,
在Rt△AEO中,OE=
=15x,
∴PE=OP-OE=25x-15x=10x,
在Rt△APE中,tan∠PAE=
=
=
,
即tan∠PAB的值为
.

∴∠BAC=60°,
∵AB=AC,
∴△ABC为等边三角形,
∴∠ACB=∠ABC=60°,
∴∠APC=∠ABC=60°,
而点P是
 |
| AB |
∴∠ACP=
| 1 |
| 2 |
∴∠PAC=90°,
∴tan∠PCA=
| PA |
| AC |
| ||
| 3 |
∴AC=
| 3 |
(2)过A点作AD⊥BC交BC于D,连结OP交AB于E,如图,
∵AB=AC,
∴AD平分BC,

∴点O在AD上,
连结OB,则∠BOD=∠BAC,
∵∠BPC=∠BAC,
∴sin∠BOD=sin∠BPC=
| 24 |
| 25 |
| BD |
| OB |
设OB=25x,则BD=24x,
∴OD=
| OB2-BD2 |
在Rt△ABD中,AD=25x+7x=32x,BD=24x,
∴AB=
| AD2+BD2 |
∵点P是
 |
| AB |
∴OP垂直平分AB,
∴AE=
| 1 |
| 2 |
在Rt△AEO中,OE=
| AO2-AE2 |
∴PE=OP-OE=25x-15x=10x,
在Rt△APE中,tan∠PAE=
| PE |
| AE |
| 10x |
| 20x |
| 1 |
| 2 |
即tan∠PAB的值为
| 1 |
| 2 |
看了 如图,已知△ABC是O的内接...的网友还看了以下:
概率论:随机事件A,C,满足P(A|A+C)+P(C|A+C)=1下列说法正确的是a,A、C不相容 2020-06-12 …
PA,PC分别切圆O于A,C两点,B为圆O上与A,C不重合的点,若角P=50度,则角ABC=度. 2020-06-15 …
概率论与数理统计里的一道证明题设本题涉及的事件均有意义,设A,B都是事件.1.已知P(A)>0,证 2020-06-18 …
设一组初始记录关键字序列为(Q,H,C,Y,P,A,M,S,R,D,F,X),则按字母升序的第一趟 2020-07-17 …
已知:如图,直线与x轴相交于点A,与直线相交于点P。(1)求点P的坐标;(2)请判断△OPA的形状 2020-07-22 …
在证明二元函数可微充分条件的结尾,他得出差为o(p)+a(x)然后就得出结论请问这个结果怎么会等于 2020-07-25 …
如图,已知直线y1=2x-3与y2=-x+3,在平面直角坐标系中相交于点P.(1)求点P的坐标;(2 2020-11-01 …
直线y=-根号3+4根号3与x轴相交于点A,与直线y=根号3/3x相交于点P.1.求点P的坐标2.求 2020-12-15 …
已知:如图,直线与x轴相交于点A,与直线相交于点P(2,).(1)请判断的形状并说明理由.(2)动点 2020-12-15 …
x+4与x轴相交于点A,与直线y=x相交于点P.(1)求点P的坐标;(2)求S△OPA的值;(3)动 2021-01-11 …