早教吧作业答案频道 -->数学-->
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D(Ⅰ)证明:BD=DF;(Ⅱ)若∠D=∠EBC,求证:AB2BD2=AFCD.
题目详情
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D
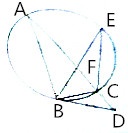
(Ⅰ)证明:BD=DF;
(Ⅱ)若∠D=∠EBC,求证:
=
.

(Ⅰ)证明:BD=DF;
(Ⅱ)若∠D=∠EBC,求证:
| AB2 |
| BD2 |
| AF |
| CD |
▼优质解答
答案和解析
证明:(Ⅰ)∵过点B作圆的切线交AC的延长线于点D,
∴∠CBD=∠A,
∵∠ABC的平分线BF交圆于点E,
∴∠ABF=∠CBF,
∵∠CFB=∠A+∠ABF,
∴∠CFB=∠DBF,
∴BD=DF;
(Ⅱ)∵BD是切线,
∴∠DBC=∠A,
又∵∠BDC=∠ADB,
∴△BDC∽△ADB,
∴
=
=
,
∴BD2=AD×DC,
=
∵∠D=∠EBC,∠CFB=∠DBF,∠ACB=∠CBD+∠D
∴△DBF∽△BCF,
∴
=
,
∵
=
,
∴
=
,
∵BF=BC,
∴
=
,
∵∠ABC的平分线BF交圆于点E,
∴利用角平分线的性质可得
=
,
∴
=
,
∴
=
,
∴AB2=AD×AF,
∵BD2=AD×DC,
∴
=
.
∴∠CBD=∠A,
∵∠ABC的平分线BF交圆于点E,
∴∠ABF=∠CBF,
∵∠CFB=∠A+∠ABF,
∴∠CFB=∠DBF,
∴BD=DF;
(Ⅱ)∵BD是切线,
∴∠DBC=∠A,
又∵∠BDC=∠ADB,
∴△BDC∽△ADB,
∴
| BD |
| AD |
| DC |
| DB |
| BC |
| AB |
∴BD2=AD×DC,
| BD |
| BC |
| AD |
| AB |
∵∠D=∠EBC,∠CFB=∠DBF,∠ACB=∠CBD+∠D
∴△DBF∽△BCF,
∴
| DB |
| BC |
| BF |
| CF |
∵
| BD |
| BC |
| AD |
| AB |
∴
| BF |
| CF |
| AD |
| AB |
∵BF=BC,
∴
| BC |
| CF |
| AD |
| AB |
∵∠ABC的平分线BF交圆于点E,
∴利用角平分线的性质可得
| AB |
| BC |
| AF |
| CF |
∴
| BC |
| CF |
| AB |
| AF |
∴
| AB |
| AF |
| AD |
| AB |
∴AB2=AD×AF,
∵BD2=AD×DC,
∴
| AB2 |
| BD2 |
| AF |
| CD |
看了 如图,△ABC为圆的内接三角...的网友还看了以下:
正切角2的平方减去正切角2的四次方的最大值是多少?一个角的正切的平方减去这个角的四次方的最大值 2020-04-12 …
如图梯形ABCD内接于圆O,DC//AB,AB=AC过A做圆O的切线与CD的延长线交于E,求证AD 2020-05-16 …
高数:求球面任意一点切面方程过单位球面x^2+y^2+z^2=1上任意一点(x0,y0,z0),和 2020-05-16 …
直角三角形中,一条直角边为a一条直角边为b斜边为c,斜边上的高为h,求证h的平方分之一等于a平方分 2020-05-22 …
在直角三角形ABC中,角C为直角,AC平分角A,交BC于D,求证AC的平方:AD的平方=BC:2B 2020-06-13 …
几何题 无图 自己构思图形1在正方形ABCD中作一点M,证明三角形ABM,BCM,CDM,DAM的 2020-06-27 …
Tan^2*也就是正切的平方是什么意思?是后面的角平方,还是正切乘以角度的积的平方? 2020-07-30 …
某学校研究性学习小组的同学做“验证力的平行四边形定则”实验(1)用平木板、细绳套、橡皮条、弹簧测力计 2020-11-01 …
怎样查询数学证明题的答案已知角ACB=90度角MCN=45度,当M,N在AB上时求证MN的平方=AN 2020-11-20 …
百思不得其解CAD怎么在圆的外面画一个与圆相切的平行四边形?知道圆的直径20知道平行四边形的线长是4 2020-12-10 …