如图，在圆内接四边形ABCD中，CD为∠BAC的外角平分线，F为AD上一点，BC=AF，延长DF与BA的延长线交于E．（1）求证：AD=BD；（2）若AC=10，AF=3，DF：FE=3：2，求DE的长．

Question

如图，在圆内接四边形ABCD中，CD为∠BAC的外角平分线，F为

AD

上一点，BC=AF，延长DF与BA的延长线交于E．

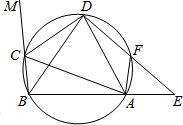
（1）求证：AD=BD；
（2）若AC=10，AF=3，DF：FE=3：2，求DE的长．

Answer 1

（1）证明：
∵CD平分∠ACM，
∴∠ACD=∠MCD，
∵四边形ABCD为圆内接四边形，
∴∠MCD=∠BAD，
又∠ACD=∠ABD，
∴∠BAD=∠ABD，
∴AD=BD；
（2）
∵BD=AD，BC=AF，
∴

BD

=

AD

，

BC

=

AF

，
∴

CD

=

DF

，
∴CD=DF，
∵BC=AF，
∴∠BDC=∠ADF，
∴∠CDA=∠BDF=∠EAF，
由（1）可知∠DCA=∠DBA，且∠EFA=∠DBA，
∴∠DCA=∠EFA，
∴△AEF∽△DAC，
∴(EF)/(AC)=(AF)/(CD)，
∴(EF)/(AC)=(AF)/(DF)，(EF)/(10)=(3)/(DF)，
∴EF•DF=30，
∵DF：FE=3：2，
∴设DF=3x，则FE=2x，
∴6x²=30，解得x=√(5)，
∴DE=DF+FE=5x=5√(5)．