早教吧作业答案频道 -->数学-->
如图,△ABC是边长为4的等边三角形,以BC为底边作一个顶角为120°的等腰三角形△DBC,以D为顶点作∠EDF=60°,使点E,F分别在边AB,边AC上运动,G在AC延长线上且CG=BE,连接EF,GD.(1)求证:
题目详情
如图,△ABC是边长为4的等边三角形,以BC为底边作一个顶角为120°的等腰三角形△DBC,以D为顶点作∠EDF=60°,使点E,F分别在边AB,边AC上运动,G在AC延长线上且CG=BE,连接EF,GD.
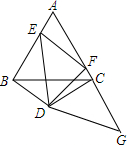
(1)求证:△BED≌△CGD;
(2)试判断当E,F点的位置变化时,是否影响△EAF周长的大小?若有影响,试说明怎样影响;若无影响,请求出△EAF的周长.

(1)求证:△BED≌△CGD;
(2)试判断当E,F点的位置变化时,是否影响△EAF周长的大小?若有影响,试说明怎样影响;若无影响,请求出△EAF的周长.
▼优质解答
答案和解析
 (1)∵△ABC为等边三角形,
(1)∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵DB=DC,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠EBD=∠GCD=90°,
在△EBD和△GCD中,
,
∴△EBD≌△GCD(SAS);
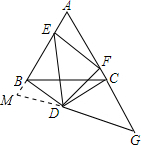
(2)当E,F点的位置变化时,不影响△EAF周长的大小,周长为8,理由为:
延长AB至M,使BM=CF,连接MD,
∵△ABC是等边三角形,
∴∠BAC=60°,
又∠BDC=120°,
∴A、B、D、C共圆,
∴∠MBD=∠FCD,
∵BM=CF,BD=CD,
∴△BDM≌△CDF,
∴DM=DF,∠BDM=∠CDF,
∵∠EDF=60°,
∴∠EDM=∠BDE+∠BDM=∠BDE+∠CDF=∠BDC-∠EDF=60°,
∴∠EDG=∠EDF,
∵DM=DF,DE=DE,
∴△EDM≌△EDF,
∴EM=EF,
∴△AEF的周长=AE+EF+AF=AE+EM+AF=AE+BE+BM+AF=AB+CF+AF=AB+AC=4+4=8.
 (1)∵△ABC为等边三角形,
(1)∵△ABC为等边三角形,∴∠ABC=∠ACB=60°,
∵DB=DC,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠EBD=∠GCD=90°,
在△EBD和△GCD中,
|
∴△EBD≌△GCD(SAS);
(2)当E,F点的位置变化时,不影响△EAF周长的大小,周长为8,理由为:
延长AB至M,使BM=CF,连接MD,
∵△ABC是等边三角形,
∴∠BAC=60°,
又∠BDC=120°,
∴A、B、D、C共圆,
∴∠MBD=∠FCD,
∵BM=CF,BD=CD,
∴△BDM≌△CDF,
∴DM=DF,∠BDM=∠CDF,
∵∠EDF=60°,
∴∠EDM=∠BDE+∠BDM=∠BDE+∠CDF=∠BDC-∠EDF=60°,
∴∠EDG=∠EDF,
∵DM=DF,DE=DE,
∴△EDM≌△EDF,
∴EM=EF,
∴△AEF的周长=AE+EF+AF=AE+EM+AF=AE+BE+BM+AF=AB+CF+AF=AB+AC=4+4=8.
看了 如图,△ABC是边长为4的等...的网友还看了以下:
anoldmanwaswaitingforaride()theriver空格应该填什么介词为什么不 2020-04-25 …
anoldmanwaswaitingforaride()theriver空格应该填什么介词为什么不 2020-04-25 …
四边形的四条边分别为a,b,c,d,其中a,c为对边,且满足a平方+b平方+c平方=2ab+2cd 2020-05-15 …
勾股定理的变形公式,知道C边和一直角边,求另一个直角边的公式 2020-06-10 …
如果四边形内的一个点到四条边的距离相等,那么这个四边形一定有()A.一组邻边相等B.一组对边平行C 2020-06-13 …
具备下列条件的三角形中,不一定全等的是A有两角和一边对应相等B两边对应相等的两个直角三角形C由两边 2020-07-21 …
RT.怎样做两个活动的平行四边形.一个邻边等,一个邻边不等.要求通俗易懂. 2020-07-30 …
正多边形与圆如果正多边形的每个外角都等于它的一个内角,那么它有《》A.3条边B.4条边C.5条边D 2020-08-01 …
高中数学题,三角函数,分配,极坐标等,求帮忙第一题将18个人分给3个宿舍,每间宿舍最少一人,且各宿舍 2020-12-06 …
在ΔABC中,已知角B=60°,边AC长为4,ΔABC的面积为根号3,求此三角形另外两边的长?AC为 2021-02-07 …