早教吧作业答案频道 -->数学-->
选修4-4:坐标系与参数方程已知直线l的参数方程为(t为参数),曲线C的参数方程为(θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).求:(1)线段AB的中点坐
题目详情
选修4-4:坐标系与参数方程
已知直线l的参数方程为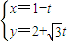 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为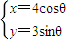 (θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).
(θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).
求:(1)线段AB的中点坐标;
(2)线段AB的长;
(3)|PA-PB|的值.
已知直线l的参数方程为
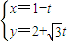 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为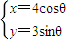 (θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).
(θ为参数),直线l与曲线C相交于A,B两点,又点P的坐标为(1,2).求:(1)线段AB的中点坐标;
(2)线段AB的长;
(3)|PA-PB|的值.
▼优质解答
答案和解析
【答案】分析:先将直线的参数方程化为(l为参数)的形式,此时,|l|的几何意义为(a,b)点到(x,y)的距离,(1)设点A对应的参数为l1,点B对应的参数为l2,将直线的参数方程代入曲线,利用韦达定理即可得l1+l2,而即为AB中点对应的参数,代入参数方程可得中点坐标;(2)AB的长度即为AB参数差的绝对值,利用韦达定理代入求值即可;因为点P(1,2)在直线上,且点P在椭圆内,故A、B两点分布在点P两侧,即l1与l2异号,所以|PA-PB|的值即为l1+l2的绝对值,代入求值即可由题意可知,直线l的斜率为-,倾斜角为∴直线l的参数方程可改写为(l为参数,|l|的几何意义为(1,2)点到(x,y)的距离),曲线C的普通方程为,将直线方程代入曲线C的方程可得,,设点A对应的参数为l1,点B对应的参数为l2,∵△>0,∴,,由参数l的几何意义得(1)中点对应的参数为,代入直线参数方程得∴线段AB中点坐标为;(2)弦AB的长为AB=|l1-l2|===;(3)∵点P(1,2)在直线上,且点P在椭圆内,故A、B两点分布在点P两侧,即l1与l2异号∴.点评:本题考查了直线的参数方程,参数的几何意义及其应用,椭圆的参数方程及其与一般方程的互化,韦达定理在解决解析几何问题中的重要应用
看了 选修4-4:坐标系与参数方程...的网友还看了以下:
直线y=2x-3与x轴交与点a与y轴交与点b直线y=负3x+b过点b且与x轴交与点c,求△abc的 2020-05-16 …
抛物线y=x^2-2x-3与x轴交与A,B两点,与y轴交与C点.设直线y=-x+3与y轴的交点抛物 2020-06-14 …
已知直线l1:y2x+4与x轴交与点A,与y轴交与点B,直线l2:y2=kx+b与l1关于x轴对称, 2020-11-11 …
已知,如图抛物线y=ax2+3ax+c(a》0)与外轴交与点C,与x交与A,B两点已知:如图,抛物线 2020-11-27 …
已知二次函数y=x的平方-4x+3图像与x轴交与A,B两点(点A在点B的左边),与y轴交与点c,顶点 2021-01-10 …
已知函数Y=X+3与Y轴分别交与A,B两点直线L过原点且与线段AB交与点C并把三角形AOB的面积分为 2021-01-10 …
直线Y=-¾X+4与Y轴交与点A与X轴交与点D与直线Y=4/5X+4/5交与点B直线Y=4/5X+4 2021-01-10 …
如图所示,已知抛物线y=x平方-1与x轴交与A,B俩点,与y轴交与点C.2011-01-041如图所 2021-01-10 …
如图所示,已知抛物线y=x平方-1与x轴交与A,B俩点,与y轴交与点C.1)求A,B,C三点坐标2) 2021-01-10 …
y=x(X的平方)-4x+3与坐标轴交与A,B,C三点,点P为抛物线上一点,PE垂直于BC与E点,且 2021-01-11 …