在极坐标系中，已知圆C的圆心C(3)，半径为1.Q点在圆周上运动，O为极点.(1)求圆C的极坐标方程；(2)若P在直线OQ上运动，且满足，求动点P的轨迹方程.

Question

在极坐标系中，已知圆C的圆心C(3 )，半径为1.Q点在圆周上运动，O为极点.

(1)求圆C的极坐标方程；

(2)若P在直线OQ上运动，且满足 ，求动点P的轨迹方程.

Answer 1

思路分析：在△OCM中 根据余弦定理 可找到圆C上的任意一点M的ρ、θ之间的关系；通过比例 可找到Q点与P点极坐标之间的关系 从而求出点P的轨迹方程.

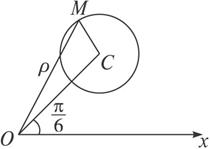
(1)设M(ρ θ)为圆C上任意一点 如图 在△OCM中 |OC|=3 |OM|=ρ |CM|=1

∠COM=|θ- | 根据余弦定理 得1=ρ ² +9-2·ρ·3·cos|θ- |.化简整理 得ρ ² -6·ρcos(θ- )+8=0为圆C的轨迹方程.

(2)设Q(ρ ₁ θ ₁ ) 则有ρ ₁ ² -6·ρ ₁ cos(θ ₁ - )+8=0.①

设P(ρ θ) 则OQ∶QP=ρ ₁ ∶(ρ-ρ ₁ )=2∶3.

∴ρ ₁ = ρ.

又θ ₁ =θ 即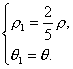

代入① 得 ρ ² -6· ρcos(θ- )+8=0.

整理 得ρ ² -15ρcos(θ- )+50=0.它为P点的轨迹方程.