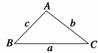
如图所示,在△ABC中,射影定理可表示为a=b·cosC+c·cosB,其中a,b,c分别为角A,B,C的对边,类比上述定理,写出对空间四面体性质的猜想.
如图所示,在△ ABC 中,射影定理可表示为 a = b ·cos C + c ·cos B ,其
中 a , b , c 分别为角 A , B , C 的对边,类比上述定理,写出对空间
四面体性质的猜想.
四边形的四条边分别为a,b,c,d,其中a,c为对边,且满足a平方+b平方+c平方=2ab+2cd 2020-05-15 …
如图△ABC的三个顶点的坐标分别为A(1,3),B(3,1),C(1,-2),试在平面直角坐标系中 2020-05-19 …
如图,已知角A、O、B=90°,角B、O、C=30°,OM平分角AOC,ON平分角B、O、C.1. 2020-06-18 …
三角形ABC的边与其他角的正弦余弦关系设以∠CAB为直角,A,B,C为三角形的顶点,三个角对应分别 2020-08-02 …
如果一个三角形的三边的长分别为a、b、c,那么可以根据秦九韶-海伦公式S=p(p−a)(p−b)(p 2020-11-03 …
甲乙两小球质量相等,将甲沿着足够长的斜面抛出,其斜面倾角为30度,乙呈30度角抛出,其抛出时速度相同 2021-01-20 …
如果两条平行直线被第三条直线所截得的8个角中有一个角的度数已知,则()A.只能求出其余3个角的度数B 2021-01-24 …
如果两条平行直线被第三条直线所截得的8个角中有一个角的度数已知,则()A.只能求出其余3个角的度数B 2021-01-24 …
已知三角形两边长度(a,b)及其夹角(∠C),能否求出第三边或者其面积或者∠A和∠B?如果已知角不是 2021-02-07 …
(2011•宿迁模拟)物体因绕轴转动时而具有的动能叫转动动能.某同学为探究转动动能的大小与角速度大小 2021-02-09 …