早教吧作业答案频道 -->数学-->
如图,已知AD是△ABC的角平分线,O经过A、B、D三点.过点B作BE∥AD,交O于点E,连接ED(1)求证:ED∥AC;(2)若BD=2CD,设△EBD的面积为S1,△ADC的面积为S2,且S12-16S2+4=0,求△ABC的面积.
题目详情
如图,已知AD是△ABC的角平分线, O经过A、B、D三点.过点B作BE∥AD,交 O于点E,连接ED
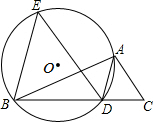
(1)求证:ED∥AC;
(2)若BD=2CD,设△EBD的面积为S1,△ADC的面积为S2,且S12-16S2+4=0,求△ABC的面积.

(1)求证:ED∥AC;
(2)若BD=2CD,设△EBD的面积为S1,△ADC的面积为S2,且S12-16S2+4=0,求△ABC的面积.
▼优质解答
答案和解析
(1)证明:∵AD是△ABC的角平分线,
∴∠BAD=∠DAC,
∵∠E=∠BAD,
∴∠E=∠DAC,
∵BE∥AD,
∴∠E=∠EDA,
∴∠EDA=∠DAC,
∴ED∥AC;
(2) ∵BE∥AD,
∴∠EBD=∠ADC,
∵∠E=∠DAC,
∴△EBD∽△ADC,且相似比k=
=2,
∴
=k2=4,即s1=4s2,
∵s12-16S2+4=0,
∴16S22-16S2+4=0,
即(4S2-2)2=0,
∴S2=
,
∵
=
=
=
=3,
∴S△ABC=
.
∴∠BAD=∠DAC,
∵∠E=∠BAD,
∴∠E=∠DAC,
∵BE∥AD,
∴∠E=∠EDA,
∴∠EDA=∠DAC,
∴ED∥AC;
(2) ∵BE∥AD,
∴∠EBD=∠ADC,
∵∠E=∠DAC,
∴△EBD∽△ADC,且相似比k=
| BD |
| DC |
∴
| S1 |
| S2 |
∵s12-16S2+4=0,
∴16S22-16S2+4=0,
即(4S2-2)2=0,
∴S2=
| 1 |
| 2 |
∵
| S△ABC |
| S2 |
| BC |
| CD |
| BD+CD |
| CD |
| 3CD |
| CD |
∴S△ABC=
| 3 |
| 2 |
看了 如图,已知AD是△ABC的角...的网友还看了以下:
如图所示,直线和抛物线(开口向上)分别为汽车a和b的位移-时间图象,则()A.0~1s时间内a车的 2020-04-07 …
物质的量习题1.相同质量的下列物质,所含分子数目最多的是A.CH4B.NH3C.H20D.HF2. 2020-05-13 …
日历:2009年9月小星期三 23辛巳年八月初五今日5:19秋分秋分时刻,太阳直射点的地理坐标为( 2020-05-16 …
利用有理数abc在数轴上的位置,化简a+|a+b|-|c|-|c-b|,将a,b,c,0,-a,- 2020-05-22 …
已知A,B均为n阶方阵,则必有()A.(A+B)2=A2+2AB+B2B.(AB)T=ATBTC. 2020-06-02 …
已知集合A{a,b,c,d,e},B{0,1,…2014},f为A→B映射,且满足f(已知集合A{ 2020-07-30 …
已知函数f(x)=exx2-k(2x+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的 2020-07-31 …
多元一次方程求解a=0.1072(a+b+c+d+e)b=0.041(a+b+c+d+e)c=0.2 2020-12-14 …
随机过程X(t)=t^2+Asint+Bcost,A、B伪随机变量,且E[A]=E[B]=0,D[A 2020-12-23 …
在1标准大气压下,下列各类物质中,放热后温度立即降低的是()A.0℃的冰B.0℃的水C.0℃的冰水混 2021-01-01 …