早教吧作业答案频道 -->数学-->
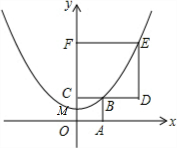
如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则FECB的值为.
题目详情
如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则
的值为___.
| FE |
| CB |

▼优质解答
答案和解析
设正方形OABC的边长为m,和正方形CDEF的边长为n.
∵点M为OC的中点,
∴点M为(0,
)、点B为(m,m)和点E为(n,m+n),
∵抛物线y=ax2+b经过M,B,E三点,
∴m=am2+
,
解得:a=
,
∴抛物线y=
x2+
,
把点E(n,m+n)代入抛物线得
m+n=
•n2+
,
解得:n=m+
m或n=m-
m(不合题意,舍去),
即CB=m,EF=m+
m,
∴
=1+
.
∵点M为OC的中点,
∴点M为(0,
| m |
| 2 |
∵抛物线y=ax2+b经过M,B,E三点,
∴m=am2+
| m |
| 2 |
解得:a=
| 1 |
| 2m |
∴抛物线y=
| 1 |
| 2m |
| m |
| 2 |
把点E(n,m+n)代入抛物线得
m+n=
| 1 |
| 2m |
| m |
| 2 |
解得:n=m+
| 2 |
| 2 |
即CB=m,EF=m+
| 2 |
∴
| FE |
| CB |
| 2 |
看了 如图,正方形OABC和正方形...的网友还看了以下:
已知函数f(x)定义域为R,且对任意实数x,y满足f(x+y)=f(x)f(y),给出以下四个结论 2020-05-13 …
f(x)+f(y)=2f[(x+y)/2]f[(x-y)/2],f(0)不等于,且存在非零常数c, 2020-05-14 …
Armstrong公理系统包括6个推理规则,下面哪一条是对伪传递规则的描述?()A.若X→Y及Y→Z 2020-05-23 …
下面哪一条是对伪传递规则的描述?()A.若X→Y及Y→Z为F所逻辑蕴含,则X→Z为F所逻辑蕴含B.由 2020-05-24 …
下面哪一条是对Armstrong公理系统中合并律的描述?()A.若X→Y及Y→Z为F所逻辑蕴含,则X 2020-05-24 …
曲面ax+by+cz=f(x2+y2+z2)的法向量与{x0,y0,z0}和{a,b,c}共面,f 2020-07-29 …
水平渐近线的问题水平渐近线的定义是若limx->无穷大f(x)=A,称y=A为f(x)的水平渐近线 2020-08-01 …
函数f(x)=ex(e为自然对数的底数)对任意实数x、y,都有()A.f(x+y)=f(x)f(y 2020-08-02 …
三元一次方程组a*x+b*y+c*z+d=0,e*x+f*y+g*z+h=0,i*x+j*y+k* 2020-08-03 …
设对任意实数x,y有[f(x)+f(y)]/2=0,f(0)=c,证明f(x)恒为c设对任意实数x, 2020-11-10 …