早教吧作业答案频道 -->数学-->
(本小题满分12分)在锐角△ABC中,分别为∠A、∠B、∠C所对的边,且(1)确定∠C的大小;(2)若c=,求△ABC周长的取值范围.
题目详情
(本小题满分12分)在锐角△ABC中,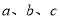 分别为∠A、∠B、∠C所对的边,且
分别为∠A、∠B、∠C所对的边,且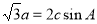
(1)确定∠C的大小;
(2)若c=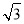 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
▼优质解答
答案和解析
(1)或;(2).
分 析:
(1)利用正弦定理,将边角关系转化为角角关系进行求解;(2)利用正弦定理用角A的三角函数表示,利用三角函数的图像与性质进行求解.解题思路: 解三角形问题,要灵活选用正弦定理、余弦定理、三角形的面积公式和内角和定理进行求解,还往往与两角和的三角公式相联系.试题
解析:
(1)已知a、b、c分别为∠A、∠B、∠C所对的边,由a=2csinA,得sinA=2sinCsinA,又sinA≠0,则sinC=,∴∠C=60°或∠C=120° ∵△ABC为锐角三角形,∴∠C=120°舍去。∴∠C=60°(2)∵c=,sinC=∴由正弦定理得: 即a=2sinA,b=2sinB,又A+B=π-C=,即B=-A,∴a+b+c=2(sinA+sinB)+=2[sinA+sin(-A)]+ =2(sinA+sincosA-cossinA)+=3sinA+cosA+=2(sinAcos+cosAsin)+=2sin(A+)+,∵△ABC是锐角三角形,∴<∠A<,∴<sin(A+)≤1,则△ABC周长的取值范围是(3+,3].
考点:
1.正弦定理;2.三角恒等变换;3.三角函数的图像与性质.
分 析:
(1)利用正弦定理,将边角关系转化为角角关系进行求解;(2)利用正弦定理用角A的三角函数表示,利用三角函数的图像与性质进行求解.解题思路: 解三角形问题,要灵活选用正弦定理、余弦定理、三角形的面积公式和内角和定理进行求解,还往往与两角和的三角公式相联系.试题
解析:
(1)已知a、b、c分别为∠A、∠B、∠C所对的边,由a=2csinA,得sinA=2sinCsinA,又sinA≠0,则sinC=,∴∠C=60°或∠C=120° ∵△ABC为锐角三角形,∴∠C=120°舍去。∴∠C=60°(2)∵c=,sinC=∴由正弦定理得: 即a=2sinA,b=2sinB,又A+B=π-C=,即B=-A,∴a+b+c=2(sinA+sinB)+=2[sinA+sin(-A)]+ =2(sinA+sincosA-cossinA)+=3sinA+cosA+=2(sinAcos+cosAsin)+=2sin(A+)+,∵△ABC是锐角三角形,∴<∠A<,∴<sin(A+)≤1,则△ABC周长的取值范围是(3+,3].
考点:
1.正弦定理;2.三角恒等变换;3.三角函数的图像与性质.
看了 (本小题满分12分)在锐角△...的网友还看了以下:
若sinA=0.4533,则锐角A≈?若cosA=0.6753则锐角A≈?若tanA若sinA=0 2020-05-17 …
在三角形ABC,角A是最小角,角B是最大角,且2倍角B=5倍角A,若角B的最大值为m度,最小值n度 2020-07-16 …
三角形ABC中,角ABC,角ACB的平分线相交于点O(1)若角ABC=40度,角ACB=50度,则 2020-07-18 …
(2b-根号3乘c)cosA=根号3乘acosc求角A若角B=30度BC边上中线为AM=(根号7) 2020-07-22 …
关于锐角三角函数.a为锐角,若tana=0.2,则a=?若cosa=0.5127,则a=a为锐角, 2020-07-30 …
利用正弦定理或余弦定理判断下列三角形的形状,谢若acosB=bcosA、则三角形abc是三角形.若 2020-08-02 …
利用正弦定理或余弦定理判断下列三角形的形状,若acosB=bcosA、则三角形abc是三角形.若a 2020-08-02 …
若角a是第一象限角,那么2a是哪个象限角?,a/2,a/3是第几象限角.若角a是第二象限角呢?若角 2020-08-03 …
在三角型abc中.若角a=2角b10度.角b=2角c-10度.则角a=?在△ABC中:(1)若∠A= 2020-10-31 …
请帮我解决几道关于三角形的数学题(1)在三角形ABC中,角A是最小角,角B是最大角,且2倍角B=5倍 2020-11-20 …