已知函数f（x）=xlnx+a（a∈R），g（x）=2xex-1-e（e为自然对数的底数）．（Ⅰ）讨论函数f（x）的零点个数；（Ⅱ）求证：当x>0时，f（x）>g（x）+a．

Question

已知函数f（x）=xlnx+a（a∈R），g（x）=(2x)/(ex-1)-e（e为自然对数的底数）．
（Ⅰ）讨论函数f（x）的零点个数；
（Ⅱ）求证：当x>0时，f（x）>g（x）+a．

Answer 1

（I）令f（x）=0得a=-xlnx，
令h（x）=-xlnx，则h′（x）=-lnx-1，
∴当0(1)/(e)时，h′（x）>0，当x>(1)/(e)时，h′（x）<0，
∴h（x）在（0，(1)/(e)）上单调递增，在（(1)/(e)，+∞）上单调递减，
∴h_max（x）=h（(1)/(e)）=(1)/(e)，
又x→0时，h（x）>0，当x→+∞时，h（x）→-∞，
∴h（x）在（(1)/(e)，+∞）上存在唯一一个零点x=1，
作出h（x）的大致函数图象如图所示：

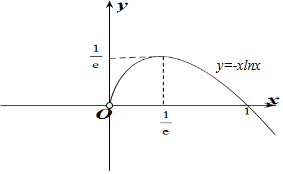
∴当a≤0或a=(1)/(e)时，f（x）有1个零点，
当0<a<(1)/(e)时，f（x）有2个零点，
当a>(1)/(e)时，f（x）没有零点．
（II）证明：∵f（x）>g（x）+a⇔xlnx>g（x），
g′（x）=(2(ex-1-xex-1))/((ex-1)2)=(2(1-x))/(ex-1)，
∴当0<x<1时，g′（x）>0，当x>1时，g′（x）<0，
∴g（x）在（0，1）上单调递增，在（1，+∞）单调递减，
∴g_max（x）=g（1）=2-e，
由（I）可知y=xlnx的最小值为-(1)/(e)，
∵-(1)/(e)-（2-e）=e-2-(1)/(e)>0，
∴xlnx-g（x）>0．即xlnx>g（x），
∴当x>0时，f（x）>g（x）+a．