早教吧作业答案频道 -->数学-->
如图,二次函数y=-ax2+2ax+c(a>0)的图象交x轴于A,B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF.(1)求A点坐
题目详情
如图,二次函数y=-ax2+2ax+c(a>0)的图象交x轴于A,B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF.
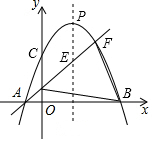
(1)求A点坐标;
(2)若△BDF的面积为12,求此二次函数的表达式;
(3)设二次函数图象顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此二次函数的表达式.

(1)求A点坐标;
(2)若△BDF的面积为12,求此二次函数的表达式;
(3)设二次函数图象顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此二次函数的表达式.
▼优质解答
答案和解析
(1)当y=0时,kx+2k=0,解得x=-2,则A(-2,0);
(2)∵二次函数y=-ax2+2ax+c(a>0)的图象的对称轴为直线x=-
=1,
∴B点坐标为(4,0),
把A(-2,0)代入y=-ax2+2ax+c得-4a-4a+c=0,
∴c=8a,
∴抛物线解析式为y=-ax2+2ax+8a,
∵DE=EF,
∴F点的横坐标为2,
∴F(2,8a),
把F(2,8a)代入y=kx+2k得8a=2k+2k,解得k=2a,
∴y=2ax+4a,
当x=0时,y=4a,则D(0,4a),
∵S△BDF=S△FAB-S△DAB,
∴
•(4+2)•8a-
•(4+2)•4a=12,解得a=1,
∴抛物线解析式为y=-x2+2x+8;
(3)抛物线的解析式表示为y=-ax2+2ax+8a,D(0,4a),F(2,8a),
当x=0时,y=-ax2+2ax+8a=8a,则C(0,8a),
当x=1时,y=-ax2+2ax+8a=9a,则P(1,9a),
∵F(2,8a),C(0,8a),
∴CF∥x轴,E(1,8a),
∴△PCF为等腰三角形,
∴PE平分∠CPF,即∠CPF=2∠CPE,
∵∠CPF=2∠DAB,
∴∠DAB=∠CPE,
∴Rt△ADO∽Rt△PCE,
∴
=
,即
=
,解得a=
或a=-
(舍去),
∴抛物线的解析式表示为y=-
x2+
x+4
.
(2)∵二次函数y=-ax2+2ax+c(a>0)的图象的对称轴为直线x=-
| 2a |
| 2×(-a) |
∴B点坐标为(4,0),
把A(-2,0)代入y=-ax2+2ax+c得-4a-4a+c=0,
∴c=8a,

∴抛物线解析式为y=-ax2+2ax+8a,
∵DE=EF,
∴F点的横坐标为2,
∴F(2,8a),
把F(2,8a)代入y=kx+2k得8a=2k+2k,解得k=2a,
∴y=2ax+4a,
当x=0时,y=4a,则D(0,4a),
∵S△BDF=S△FAB-S△DAB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴抛物线解析式为y=-x2+2x+8;
(3)抛物线的解析式表示为y=-ax2+2ax+8a,D(0,4a),F(2,8a),
当x=0时,y=-ax2+2ax+8a=8a,则C(0,8a),
当x=1时,y=-ax2+2ax+8a=9a,则P(1,9a),
∵F(2,8a),C(0,8a),
∴CF∥x轴,E(1,8a),
∴△PCF为等腰三角形,
∴PE平分∠CPF,即∠CPF=2∠CPE,
∵∠CPF=2∠DAB,
∴∠DAB=∠CPE,
∴Rt△ADO∽Rt△PCE,
∴
| AO |
| PE |
| OD |
| CE |
| 2 |
| a |
| 4a |
| 1 |
| ||
| 2 |
| ||
| 2 |
∴抛物线的解析式表示为y=-
| ||
| 2 |
| 2 |
| 2 |
看了 如图,二次函数y=-ax2+...的网友还看了以下:
已知直线y=x与直线y=kx+b交于点A(m,n)(m>0),点B在直线y=x上且与点A关于坐标原 2020-06-14 …
如图,点O是坐标系原点,直线y=kx+b与x轴交于点A,与直线y=-x+5交于点B,点B的纵坐标是 2020-06-14 …
函数1.已知直线y=-2x+6上点A的横坐标为2,直线y=kx+b经过点A与x轴交于点B(1/2, 2020-06-14 …
如图,直线y=kx+4(k≠0)与x轴,y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与 2020-07-21 …
已知:如图,在直角坐标平面中,点A在x轴的负半轴上,直线y=kx+3经过点A,与y轴相交于点M,点 2020-07-29 …
如图,Rt△AOB在直角坐标系中,OB=2,OA=4,直线y=kx(k>0)与AB交于点C,若直线 2020-07-30 …
如图,在平面直角坐标系xOy中,直线y=-3x+m与双曲线y=kx相交于点A(m,2).(1)求双 2020-07-30 …
在平面直角坐标系中,直线y=kx+b经过点(2,3)和点(-1,-3),直线y=mx与直线y=kx+ 2020-11-03 …
2011年西安世界园艺博览会于北京时间4月28日开幕,此时晨昏线m和经线n垂直交于点O,且极点P位于 2020-11-10 …
(吉林省2013年高三复习质量监测数学(理)试题)已知互相垂直的两条直线y=kx和y=-kx分别与双 2020-12-31 …