已知M为双曲线C：x2a2-y2b2=1右支上一点，A，F分别为双曲线C左顶点和的右焦点，MF=AF，若∠MFA=60°，则双曲线C的离心率为（）A.2B.3C.4D.6

Question

已知M为双曲线C：

(x2)/(a2)-(y2)/(b2)=1右支上一点，A，F分别为双曲线C左顶点和的右焦点，MF=AF，若∠MFA=60°，则双曲线C的离心率为（　　）

A. 2

B. 3

C. 4

D. 6

Answer 1

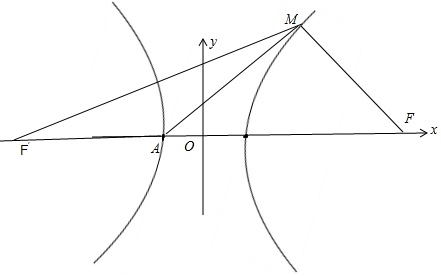如图所示，∵MF=FA，∠MFA=60°，
∴△MFA是等边三角形．
则有AF=a+c，MF=a+c，
设双曲线的另一焦点为F′，根据双曲线的定义得MF′=3a+c，
在△MFF′中，由余弦定理得MF′²=MF²+FF′²-2MF•FF′cos60°，
即4a²+3ac-c²=0，解得4a=c，即(c)/(a)=4，
∴双曲线C的离心率为4．
故选：C．