早教吧作业答案频道 -->数学-->
如图,一次函数y=-(b+2)x+b的图象经过点A(-1,0),且与y轴相较于点C,与双曲线y=kx相交于点P.(1)求b的值;(2)作PM⊥PC交y轴于点M,已知S△MPC=4,求双曲线的解析式.
题目详情
如图,一次函数y=-(b+2)x+b的图象经过点A(-1,0),且与y轴相较于点C,与双曲线y=
相交于点P.
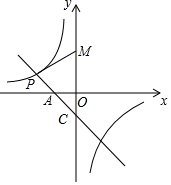
(1)求b的值;
(2)作PM⊥PC交y轴于点M,已知S△MPC=4,求双曲线的解析式.
| k |
| x |

(1)求b的值;
(2)作PM⊥PC交y轴于点M,已知S△MPC=4,求双曲线的解析式.
▼优质解答
答案和解析
(1)∵一次函数y=-(b+2)x+b的图象经过点A(-1,0),
∴b+2+b=0,
解得:b=-1.
(2)过点P作PB⊥MC于点B,如图所示.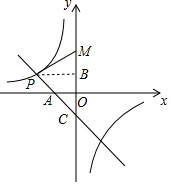
将b=-1代入一次函数解析式,得:y=-x-1.
当x=0时,y=-1,
∴点C的坐标为(0,-1),
∴OC=1,
∵点A的坐标为(-1,0),
∴OA=1=OC,
∴∠ACO=45°.
∵PM⊥PC,
∴△PMC为等腰直角三角形,
∵PB⊥MC,
∴PB=
MC,
∴S△PMC=
CM•PB=PB2,
∵S△PMC=4,
∴PB2=4,即PB=2或PB=-2(舍去),
∵点P在第二象限,
∴点P的横坐标为-2,
当x=-2时,y=-(-2)-1=1,
∴点P的坐标为(-2,1).
∵双曲线y=
经过点P,
∴k=-2×1=-2,
∴双曲线的解析式为y=-
.
∴b+2+b=0,
解得:b=-1.
(2)过点P作PB⊥MC于点B,如图所示.

将b=-1代入一次函数解析式,得:y=-x-1.
当x=0时,y=-1,
∴点C的坐标为(0,-1),
∴OC=1,
∵点A的坐标为(-1,0),
∴OA=1=OC,
∴∠ACO=45°.
∵PM⊥PC,
∴△PMC为等腰直角三角形,
∵PB⊥MC,
∴PB=
| 1 |
| 2 |
∴S△PMC=
| 1 |
| 2 |
∵S△PMC=4,
∴PB2=4,即PB=2或PB=-2(舍去),
∵点P在第二象限,
∴点P的横坐标为-2,
当x=-2时,y=-(-2)-1=1,
∴点P的坐标为(-2,1).
∵双曲线y=
| k |
| x |
∴k=-2×1=-2,
∴双曲线的解析式为y=-
| 2 |
| x |
看了 如图,一次函数y=-(b+2...的网友还看了以下:
已知直线y=x与双曲线y=k/x(k>0)的一个交点为A,且OA=2,求反比例函数的解析式已知直线 2020-05-20 …
双曲线Y=5/X在第一象限的一分支上有一点C(1.5),过点C的直线CA:Y=KX+B与X轴相交于 2020-06-04 …
如图,一次函数y=-4x-4的图象与x轴、y轴分别交于A、C两点,抛物线y=43x2+bx+c的图 2020-06-12 …
已知直线L1:y1=k1x-5L2:y2=k2x+7与y轴交于点A,C在第三象限已知直线L1:y1 2020-06-14 …
求下列一次函数的解析式1.函数的图象过点(1,-1)且与直线2x+y=5平行2.函数的图象和直线y 2020-07-09 …
-在函数y=2的x次方的图象上求一点,使过此点的切线满足下列条件:平行于直线xIn4-y+3=0在 2020-07-23 …
平面直角坐标系知识,会的进来!若A(-3a-1,2b-2)在第一象限,B点在第四象限,且过A‘B的 2020-07-26 …
高等数学设位于第一象限的曲线y=f(x)过点(√2/2,½),其中任一点P(x,y)处的法线与y轴 2020-07-30 …
设位于第一象限的曲线y=f(x)过点,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被 2020-07-31 …
如图,分别位于反比例函数y=1x,y=kx在第一象限图象上的两点A、B,与原点O在同一直线上,且O 2020-08-01 …