早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(0,4),点M是线段AB上任意一点(A,B两点除外).(1)求直线AB的解析式;(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB
题目详情
在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(0,4),点M是线段AB上任意一点(A,B两点除外).
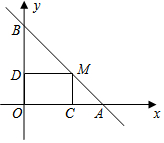
(1)求直线AB的解析式;
(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(3)当点M把线段AB分成的两部分的比为1:3时,请求出点M的坐标.

(1)求直线AB的解析式;
(2)过点M分别作MC⊥OA于点C,MD⊥OB于点D,当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(3)当点M把线段AB分成的两部分的比为1:3时,请求出点M的坐标.
▼优质解答
答案和解析
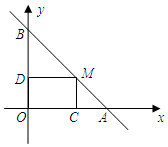
(1)设直线AB的解析式为y=kx+b,
由题意可得
,解得
,
∴AB的解析式为y=-x+4;
(2)不发生变化.
理由如下:
设M点的坐标为(x,-x+4)
MD=|x|=x,MC=|-x+4|=-x+4
四边形OCMD的周长=2(MD+MC)=2[x+(-x+4)]=8
∴四边形OCMD的周长不发生变化;
(3)∵DM∥x轴
∴
=
①当BM:MA=1:3时,
=
=
,即
=
,DM=1,
则点M的横坐标为1,此时纵坐标=-x+4=-1+4=3,M(1,3);
②当BM:MA=3:1时,
=
=
,即
=
,DM=3,
则点M的横坐标为3,此时纵坐标=-x+4=-3+4=1,M(3,1);
综上可知点M的坐标为(1,3)或(3,1).

(1)设直线AB的解析式为y=kx+b,
由题意可得
|
|
∴AB的解析式为y=-x+4;
(2)不发生变化.
理由如下:
设M点的坐标为(x,-x+4)
MD=|x|=x,MC=|-x+4|=-x+4
四边形OCMD的周长=2(MD+MC)=2[x+(-x+4)]=8
∴四边形OCMD的周长不发生变化;
(3)∵DM∥x轴
∴
| DM |
| OA |
| BM |
| BA |
①当BM:MA=1:3时,
| DM |
| OA |
| BM |
| BA |
| 1 |
| 4 |
| DM |
| 4 |
| 1 |
| 4 |
则点M的横坐标为1,此时纵坐标=-x+4=-1+4=3,M(1,3);
②当BM:MA=3:1时,
| DM |
| OA |
| BM |
| BA |
| 3 |
| 4 |
| DM |
| 4 |
| 3 |
| 4 |
则点M的横坐标为3,此时纵坐标=-x+4=-3+4=1,M(3,1);
综上可知点M的坐标为(1,3)或(3,1).
看了 在平面直角坐标系中,点A的坐...的网友还看了以下:
椭圆X^2/a^2+y^2/b^2=1(a>b>0)的一个焦点是F(1,0),O为坐标原点.设过点 2020-05-16 …
已知双曲线C:x2a2-y2b2=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与 2020-05-17 …
已知a大于等于0,函数f(x)=x^2+ax.设x1属于(负无穷,-a/2),记曲线y=f(x)在 2020-05-23 …
数形结合的综合题目(过程要完整啊)在平面直角坐标系中点O为坐标原点,以点A(0,-3)为圆心,5为 2020-06-02 …
已知三个向量与它们的坐标,要证明这三个向量在同一条直线上怎么证?忘了…这道题是这样的:OA=(1, 2020-07-10 …
如图,已知双曲线C:x2a2-y2b2=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心 2020-07-14 …
A1、A2为x2/a2+y2/b2=1)左右顶点椭圆丄异于A1A2的P,向量POPA=0求椭圆离心 2020-08-02 …
在直角坐标系中,ΔABO的顶点A坐标为A(6,0),O为原点,AB=8,∠BAO=60度,ΔABO绕 2020-11-04 …
尺规作图,角(锐角)OAB以O为圆心,任意长为半径用圆规画弧,分别叫OA,OB于点C、D.任意画一点 2020-11-26 …
如图,反比例函数y=kx(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐 2020-11-28 …