早教吧作业答案频道 -->数学-->
发现问题如图①,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点,求证:△DFM≌△MGE.拓展探究如图
题目详情
【发现问题】如图①,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点,求证:△DFM≌△MGE.
【拓展探究】如图②,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°.点F、M、G分别为AB、BC、AC边的中点,若AD=5,AB=6,△DFM的面积为a,直接写出△MGE的面积.
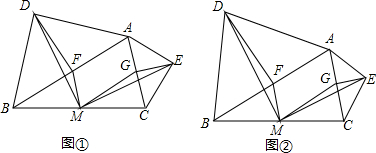
【拓展探究】如图②,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°.点F、M、G分别为AB、BC、AC边的中点,若AD=5,AB=6,△DFM的面积为a,直接写出△MGE的面积.

▼优质解答
答案和解析
【发现问题】证明:∵△ADB是等腰直角三角形,F为斜边AB的中点,
∴∠DFB=90°,DF=FA;
∵△ACE是等腰直角三角形,G为斜边AC的中点,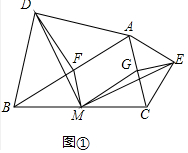
∴∠EGC=90°,AG=GE,
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴FM=AG,MG=FA,∠BFM=∠BAC,∠BAC=∠MGC,
∴DF=MG,∠DFM=∠MGE,FM=GE,
在△DFM与△MGE中,
,
∴△DFM≌△MGE.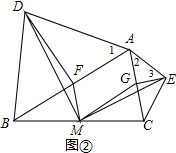
【拓展探究】∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=
AC=AG,MG=
AB=AF,∠MGC=∠BAC=∠BFM,
∴∠DFM=∠MGE,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∴tan∠1=tan∠3,
即
=
,
∴
=
,
∵∠DFM=∠MGE,
∴△DFM∽△MGE,
∴
=(
)2,
在Rt△ADF中,DF=
=
=4,
∴
=(
)2=
,
∵△DFM的面积为a,
∴S△MGE=
a.
∴∠DFB=90°,DF=FA;
∵△ACE是等腰直角三角形,G为斜边AC的中点,

∴∠EGC=90°,AG=GE,
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴FM=AG,MG=FA,∠BFM=∠BAC,∠BAC=∠MGC,
∴DF=MG,∠DFM=∠MGE,FM=GE,
在△DFM与△MGE中,
|
∴△DFM≌△MGE.

【拓展探究】∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DFM=∠MGE,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∴tan∠1=tan∠3,
即
| DF |
| AF |
| AG |
| EG |
∴
| DF |
| MG |
| FM |
| EG |
∵∠DFM=∠MGE,
∴△DFM∽△MGE,
∴
| S△MGE |
| S△DMF |
| DF |
| MG |
在Rt△ADF中,DF=
| AD2-AF2 |
| 52-32 |
∴
| S△MGE |
| S△DMF |
| MG |
| DF |
| 9 |
| 16 |
∵△DFM的面积为a,
∴S△MGE=
| 9 |
| 16 |
看了 发现问题如图①,在△ABC中...的网友还看了以下:
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0).分别过点A,点B作x轴的垂线,交抛物 2020-05-14 …
抢筑土料子埝的取土地点( )。A.距堤脚 30 m 以外B.距堤脚 20 m 以外C.借用背水坡浸润 2020-05-27 …
设a>b>c且1/a-b+1/b-c≥m/a-c恒成立,则M的范围1除以a-b的商+1除以b-c的 2020-06-27 …
如图1,直线y=-33x+3与两坐标轴交于A、B,以点M(1,0)为圆心,MO为半径作小⊙M,又以 2020-07-22 …
设集合M={a,b},N={c,d},定义M与N的一个运算“•”为:M•N={x|x=mn,m∈M 2020-07-30 …
A{n│n=2k+1,k∈Z}、B{m│m=2l-1,l∈Z}如果n∈A,那么存在k∈Z,使n=2k 2020-10-31 …
关于直线a,b,c以及平面M,N,给出下面命题:①若a∥M,b∥M,则a∥b②若a∥M,b⊥M,则b 2020-11-02 …
设集合A={x|x+m≥0},B={x|-2<x<4},全集U=R,且(∁UA)∩B=∅,求实数m的 2020-11-13 …
若数对(a,b)(a>1,b>1,a,b∈N*),对于∀m∈Z,∃x,y∈Z,使m=xa+yb成立, 2020-11-17 …
已知A、B是线段MN上的两点,MN=4,MA=1,MB>1,以A为中心顺时针旋转点M,以B为中心逆时 2020-12-21 …