早教吧作业答案频道 -->数学-->
如图,△ABC中,DE是一条中位线,延长DE到点F,使EF=DE,连接CF.(1)判断线段AD与CF的数量关系与位置关系,并证明你的猜想;(2)若AC=BC,连接DC,AF,求证:四边形ADCF是矩形.
题目详情
如图,△ABC中,DE是一条中位线,延长DE到点F,使EF=DE,连接CF.
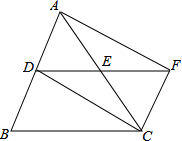
(1)判断线段AD与CF的数量关系与位置关系,并证明你的猜想;
(2)若AC=BC,连接DC,AF,求证:四边形ADCF是矩形.

(1)判断线段AD与CF的数量关系与位置关系,并证明你的猜想;
(2)若AC=BC,连接DC,AF,求证:四边形ADCF是矩形.
▼优质解答
答案和解析
证明:(1)∵DE是中位线,
∴AE=EC,
∵∠AED=∠CEF,DE=EF,
∴△AED≌△CEF,
∴AD=CF,∠A=∠ACF,
∴AD∥CF,
即:AD=CF,AD∥CF;
(2)∵AD=CF,AD∥CF,
∴四边形ADCF是平行四边形,
∵AC=BC,AD=DB,
∴CD⊥AB,
∴∠ADC=90°,
∴平行四边形ADCF是矩形.
∴AE=EC,
∵∠AED=∠CEF,DE=EF,
∴△AED≌△CEF,
∴AD=CF,∠A=∠ACF,
∴AD∥CF,
即:AD=CF,AD∥CF;
(2)∵AD=CF,AD∥CF,
∴四边形ADCF是平行四边形,
∵AC=BC,AD=DB,
∴CD⊥AB,
∴∠ADC=90°,
∴平行四边形ADCF是矩形.
看了 如图,△ABC中,DE是一条...的网友还看了以下:
一个高一证明题设x1与x2分别是实系数方程ax²+bx+c=0和-ax²+bx+c=0的一个根,且 2020-05-13 …
身份认证的含义是____。A.注册一个用户B.标识一个用户C.验证一个用户D.授权一个用户 2020-05-23 …
唯物辩证法认为,因果联系是A.事物之间的一种内在的本质联系B.事物之间的一种外在的联系C.事物之间 2020-06-07 …
不等式证明和三角形的关系.1.已知△ABC的外接圆半径R=1,S△ABC=1/4a,b,c是△AB 2020-07-24 …
用反证法证明:若整系数一元二次方程ax^2+bx+c=0(a≠0)有有理数根,求证:a,b,c中至 2020-08-01 …
用反证法证明命题:“若整数系数一元二次方程ax2+bx+c=0(a≠o)有有理根,那么a,b,c中 2020-08-01 …
如图所示,在静止的木箱内用细绳b、c系住一个小球d,细绳b水平,细绳c与竖直方向成θ角.当系统静止不 2020-12-25 …
如图所示,在静止的木箱内用细绳b、c系住一个小球d,细绳b水平,细绳c与竖直方向成θ角。当系统静止不 2020-12-25 …
如图所示,在静止的木箱内用细绳b、c系住一个小球d,细绳b水平,细绳c与竖直方向成θ角.当系统静止不 2020-12-25 …
用反证法证明:若整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,那么a、b、c中至少有一 2021-02-02 …