早教吧作业答案频道 -->数学-->
如图1,抛物线y=-x2+6x与x轴交于O、A两点,点P在抛物线上,过点P的直线y=x+m与抛物线的对称轴交于点Q.(1)这条抛物线的对称轴是:直线,直线PQ与x轴所夹锐角的度数是度;(2)若S△PO
题目详情
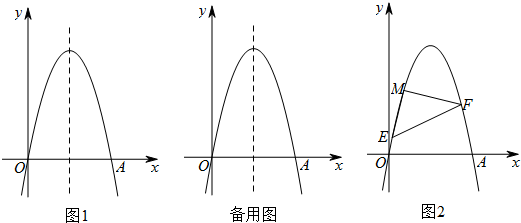
如图1,抛物线y=-x2+6x与x轴交于O、A两点,点P在抛物线上,过点P的直线y=x+m与抛物线的对称轴交于点Q.
(1)这条抛物线的对称轴是:直线___,直线PQ与x轴所夹锐角的度数是___度;
(2)若S△POQ:S△PAQ=1:2,求此时的点P坐标;
(3)如图2,点M(1,5)在抛物线上,以点M为直角顶点作Rt△MEF,且E、F均在抛物线上,则所有满足条件的直线EF必然经过定点N,求点N坐标.
(1)这条抛物线的对称轴是:直线___,直线PQ与x轴所夹锐角的度数是___度;
(2)若S△POQ:S△PAQ=1:2,求此时的点P坐标;
(3)如图2,点M(1,5)在抛物线上,以点M为直角顶点作Rt△MEF,且E、F均在抛物线上,则所有满足条件的直线EF必然经过定点N,求点N坐标.

▼优质解答
答案和解析
(1)抛物线y=-x2+6x的对称轴x=-
=3,
∵直线PQ:y=x+m与直线y=x平行,
直线y=x是一、三象限的平分线,
∴直线PQ与x轴所夹锐角的度数是45°,
故答案为x=3,45.
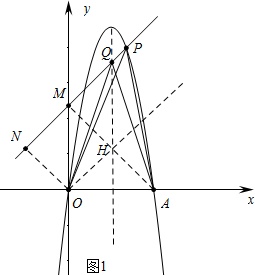
(2)如图1中,作直线y=x交对称轴于H,连接AH,延长AH交直线PQ于M,作ON⊥PQ于N则四边形ONMH是矩形.△AOH是等腰直角三角形.
∵S△POQ:S△PAQ=1:2,
∴AM=2ON,
∴ON=MH=AH,
∵点A(6,0),H(3,3),
∴点M(0,6),
∴直线PQ的解析式为y=x+6,
由
解得
或
,
∴点P坐标(2,4)或(3,3).
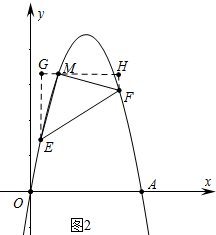
(3)如图2中,过点M作GH∥OA,过点E作EG⊥GH于G,过点F作FH⊥GH于H.
∵∠EMF=90°,
∴∠EMG+∠FMH=90°,
∵∠FMH+∠MFH=90°
∴∠EMG=∠MFH,∵∠G=∠H=90°,
∴△EMG∽△MFH,
∴
=
,设E(x1,y1)、F(x2,y2),直线EF的解析式为y=mx+n,
∴
=
,
∵y1=-x12+6x1,y2=-x22+6x2代入上式整理得到x1x2-5(x1+x2)+26=0
由
| 6 |
| 2×(-1) |
∵直线PQ:y=x+m与直线y=x平行,
直线y=x是一、三象限的平分线,
∴直线PQ与x轴所夹锐角的度数是45°,
故答案为x=3,45.
(2)如图1中,作直线y=x交对称轴于H,连接AH,延长AH交直线PQ于M,作ON⊥PQ于N则四边形ONMH是矩形.△AOH是等腰直角三角形.

∵S△POQ:S△PAQ=1:2,
∴AM=2ON,
∴ON=MH=AH,
∵点A(6,0),H(3,3),
∴点M(0,6),
∴直线PQ的解析式为y=x+6,
由
|
|
|
∴点P坐标(2,4)或(3,3).
(3)如图2中,过点M作GH∥OA,过点E作EG⊥GH于G,过点F作FH⊥GH于H.

∵∠EMF=90°,
∴∠EMG+∠FMH=90°,
∵∠FMH+∠MFH=90°
∴∠EMG=∠MFH,∵∠G=∠H=90°,
∴△EMG∽△MFH,
∴
| GM |
| FH |
| GE |
| MH |
∴
| 1-x1 |
| 5-y2 |
| 5-y1 |
| x2-1 |
∵y1=-x12+6x1,y2=-x22+6x2代入上式整理得到x1x2-5(x1+x2)+26=0
由
|
看了 如图1,抛物线y=-x2+6...的网友还看了以下:
我们将点P(x,y)经过矩阵的变换得到新的点P'(x',y')称作一次运动,即:.(1)若点P(3 2020-05-13 …
2011年 东营中考数学题如图,直线与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆 2020-05-16 …
点p(x.,y.)在圆O:x的平方+y的平方=r的平方内,则直线x.x+y.y=r的平方与已知圆O 2020-05-20 …
已知函数f(x)=ax^3+bx²,曲线y=f(x)过点P(-1,2),且在点P处的切线恰好与直线 2020-05-21 …
在平面直角坐标系中,点P(a,b)到直线x=2的距离为3,则a的值若x轴的点p到y轴的距离为3,则 2020-06-14 …
平面直角坐标系xOy中,点P(x,y)满足x≥0y≥0x6+y4≤1,当x,y均为整数时称点P(x 2020-06-14 …
数轴上两点A,B对应的书分别为-1,4,点p为数轴上一动点,其对应的数为x若点p到点a,点b的距离 2020-06-26 …
如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点,若使点P, 2020-07-07 …
下列对应法则f中,构成从集合P到S的映射的是AP=R,S=(-∞,0),x∈P,y∈S,f:x→y 2020-07-30 …
△ABC为等腰直角三角形,AB=BC=1,∠ABC=90°,动点P从A开始,沿A到C到B到A移动,设 2020-11-01 …
 扫描下载二维码
扫描下载二维码
