早教吧作业答案频道 -->数学-->
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.例如:如图四边形ABCD的内角和:N=∠A+∠B+∠C+∠D=(4-2)×180°=360
题目详情
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.
例如:如图四边形ABCD的内角和:
N=∠A+∠B+∠C+∠D=(4-2)×180°=360°
问:(1)利用这个关系式计算五边形的内角和;
(2)当一个多边形的内角和N=720°时,求其边数n.
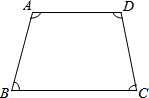
例如:如图四边形ABCD的内角和:
N=∠A+∠B+∠C+∠D=(4-2)×180°=360°
问:(1)利用这个关系式计算五边形的内角和;
(2)当一个多边形的内角和N=720°时,求其边数n.

▼优质解答
答案和解析
(1)N=(5-2)×180°=540°
(2)根据题意得:(n-2)×180°=720°
解得n=6.
(2)根据题意得:(n-2)×180°=720°
解得n=6.
看了 多边形的内角和随着边数的变化...的网友还看了以下:
一个等腰三角形,底角与顶角的比是5比2,底角与顶角多少度?要用按比例分配的方法求。 2020-05-13 …
1在钟表上,3点30分时,时针与分针的夹角多少度?2已知一个角的余角比这个角的补角的1/4小12° 2020-05-17 …
一个锐角与一个钝角互为邻角过顶点做公共边的垂线,此垂线与锐角的另一个边构成(5/7)倍直角,与钝角 2020-06-27 …
1.一个多变形除了一个内角之外,其余内角和为2570°,这个内角多少度?2.和多边形的一个内角相邻 2020-07-24 …
多边形的内角与外角关系1.多边形的内角中,最多有()个直角;2.一个多边形的内角中,锐角的个数最多 2020-07-30 …
怎样求角的余角与补角我是初一的.不会求角的余角与补角.比如是一个角的余角等于它的补角,这个角是什么 2020-07-30 …
若θ角的终边与60度角的终边相同,则终边与θ/3角的终边相同的钝角为多少度若θ角的终边与60度角的 2020-07-30 …
1、有一个N边形的内角与外角和的比是9:2,求N边形的边数2、两个多边形边数之比是1:2内角和是3: 2020-10-31 …
一个多边形的内角和是外角和的一半,求边数?一个多边形的内角和是外角和的2倍,求边数和对角线总数.一个 2020-11-18 …
关于三角形的数学题1:已知一个多边形内角和与外角和之比为11比2.(1)求这个多边形的内角和(2)求 2021-02-21 …