早教吧作业答案频道 -->数学-->
如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.(1)求证:∠ECD=∠EDC;(2)若tanA=14,求DE长;(3)当∠A从1
题目详情
如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
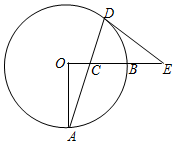
(1)求证:∠ECD=∠EDC;
(2)若tanA=
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.

(1)求证:∠ECD=∠EDC;
(2)若tanA=
| 1 |
| 4 |
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
▼优质解答
答案和解析
 (1)证明:连结OD,
(1)证明:连结OD,
∵DE是⊙O的切线,
∴∠EDC+∠ODA=90°,
∵OA⊥OB,
∴∠ACO+∠A=90°,
∵OA=OD,
∴∠ODA=∠A,
∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,
∴∠ECD=∠EDC.
(2) ∵tanA=
,
∴
=
,
∴OC=2,
设DE=x,
∵∠ECD=∠EDC,
∴CE=x,
∴OE=2+x.
∴∠ODE=90°,
∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,
∴DE=CE=15.
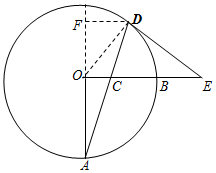
(3) 过点D作AO的垂线,交AO的延长于F,
当∠A=15°时,∠DOF=30°,DF=4,
S弓形ABD=
-
×8×4=
-16
当∠A=30°时,∠DOF=60°,DF=4
,
S弓形ABD=
-
×8×4
=
-16
,
∴S=(
-16)-(
-16
)=
π+16
-16
 (1)证明:连结OD,
(1)证明:连结OD,∵DE是⊙O的切线,
∴∠EDC+∠ODA=90°,
∵OA⊥OB,
∴∠ACO+∠A=90°,
∵OA=OD,
∴∠ODA=∠A,
∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,
∴∠ECD=∠EDC.
(2) ∵tanA=
| OC |
| OA |
∴
| OC |
| 8 |
| 1 |
| 4 |
∴OC=2,
设DE=x,
∵∠ECD=∠EDC,
∴CE=x,
∴OE=2+x.
∴∠ODE=90°,
∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,
∴DE=CE=15.
(3) 过点D作AO的垂线,交AO的延长于F,
当∠A=15°时,∠DOF=30°,DF=4,
S弓形ABD=
| 150π•64 |
| 360 |
| 1 |
| 2 |
| 80π |
| 3 |
当∠A=30°时,∠DOF=60°,DF=4
| 3 |
S弓形ABD=
| 120π•64 |
| 360 |
| 1 |
| 2 |
| 3 |
| 64π |
| 3 |
| 3 |
∴S=(
| 80π |
| 3 |
| 64π |
| 3 |
| 3 |
| 16 |
| 3 |
| 3 |
看了 如图,OA,OB是⊙O的两条...的网友还看了以下:
某次考试A、B、C、D、E五人的成绩统计如下:A、B、C、D的平均分是75分;A、C、D、E的平均分 2020-03-31 …
在正三棱锥P-ABC,AB=PA=8,过A作与PB,PC分别交于D和E的截面,则截面三角形ADE的 2020-05-14 …
如图,一个长方形被分为面积比为5:6:7:8:9的A、B、C、D、E五块,其中A和B是长方形,且A 2020-05-16 …
如图,一个长方形被分为面积比为5:6:7:8:9的A、B、C、D、E五块,其中A和B是长方形,且A 2020-06-12 …
如图,抛物线y=12x2-x-32与x轴交于A、B两点,D为y轴上一点,E为抛物线上一点,是否存在 2020-06-14 …
如图,抛物线y=12x2-x-32与x轴交于A、B两点,D为y轴上一点,E为抛物线上一点,是否存在 2020-06-14 …
设E是平面的有界闭集,d是E的直径,及d是E中任意两点距离的上确界,求证,在E中存在两点P1,P2 2020-06-23 …
如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含 2020-07-26 …
若abcd都是整数,其中c>0,并且满足a+b+c=d,b+c+d=e,c+d+e=a,e+a=b 2020-07-30 …
已知5个正数a,b,c,d,e的平均数为m,且a<b<c<d<e,则数据a,b,0,c,d,e的平均 2020-10-31 …